Del 1
Oppgave 1
Hvis prisene og antall sjokolader er proporsjonale størrelser, så skal vi få det samme svaret hvis vi deler pris på antall sjokolader for alle tilbudene
| Pris | Sjokolader | Forhold |
|---|---|---|
| 25 | 2 | 12,5 |
| 100 | 8 | 12,5 |
| 200 | 16 | 12,5 |
| 300 | 24 | 12,5 |
Prisen per sjokolade er 12,5 kroner uansett hvilket tilbud vi ser på.
Antall sjokolader og prisen du betaler er proporsjonale størrelser.
I denne oppgaveteksten så spør de om antall sjokolader og prisen du betaler for hver sjokolade. Disse to størrelsene er egentlig ikke proporsjonale siden prisen per sjokolade er 12,5 kroner uansett.
Oppgave 2
- 32 kroner for 2 bagetter betyr at hver bagett koster 16 kroner.
- 48 kroner for 4 bagetter betyr at hver bagett koster 12 kroner.
For å regne den prosentvise forskjellen kan vi sammenligne differansen mellom de to tilbudene og den dyreste prisen.
Prisen per bagett blir 25 % lavere dersom hun kjøper 4 istedenfor 2 bagetter.
Oppgave 3
For å finne den totale mengden vann på en måned må vi regne ut
I Oslo bruker man
Oppgave 4
1-4a
Jeg fortsetter mønsteret, som jeg ser består av to kvadrater hvor kvadratene overlapper med en sirkel.
Det er
Det er
1-4b
Hver figur består av to kvadrater, hvor det er én mer sirkel i sidekanten enn figurnummeret. I figur
Del 2
Oppgave 1
2-1a
Hvis det bare 1 person som skal på hyttetur så blir prisen per person
Det koster altså 18 000 kr å leie hytta.
I tillegg får vi oppgitt definisjonsmengden
Det koster 18 000 kroner å leie hytta, og det er maksimalt 12 venner som kan dra på hyttetur.
2-1b
Jeg legger inn funksjonsuttrykket i GeoGebra og avgrenser funksjonen til definisjonsmengden ved å bruke Funksjon()-kommandoen. Deretter legger jeg inn
Skjæringspunktet mellom grafen og den rette linja er
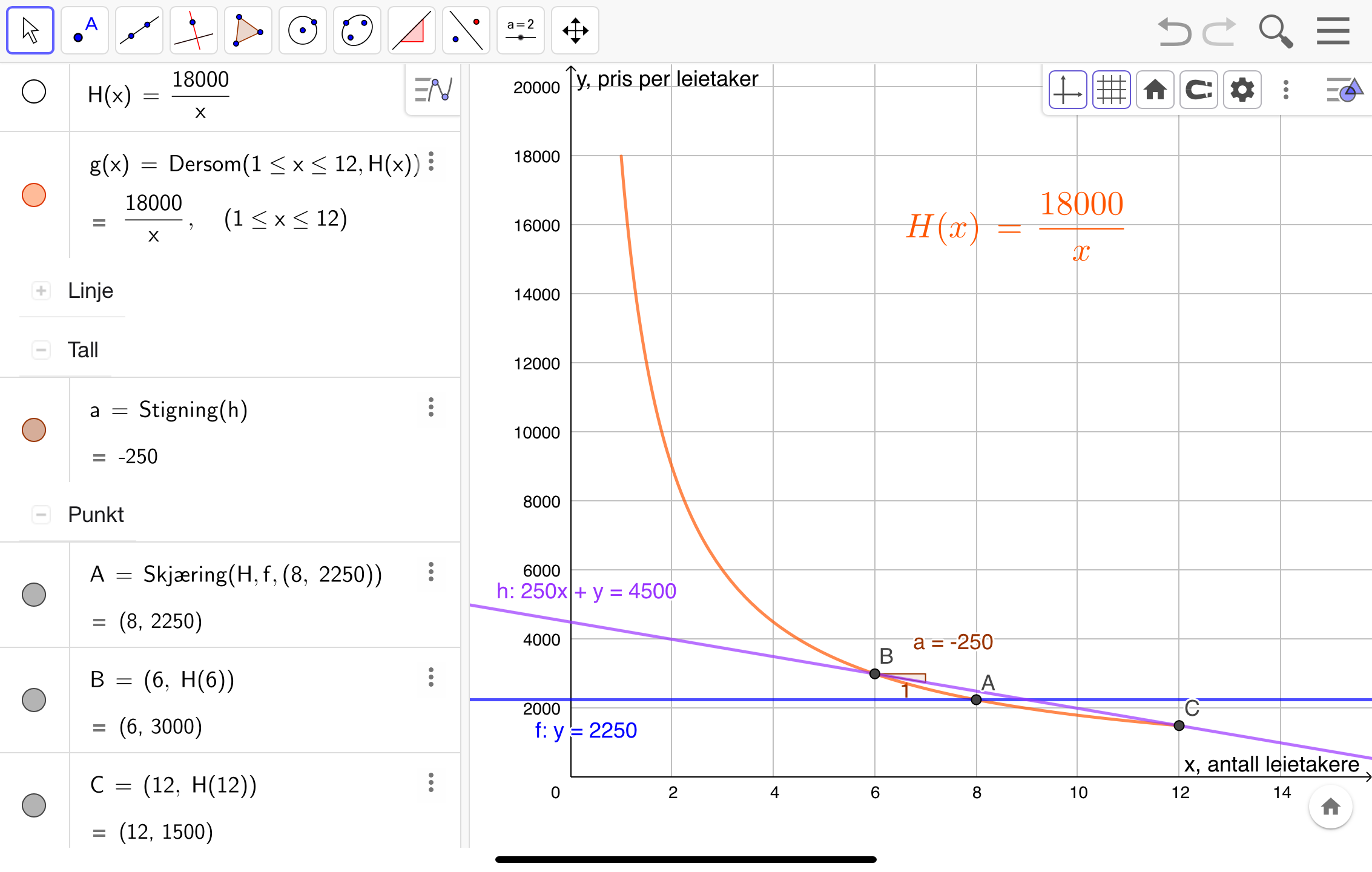
2-1c
Jeg setter ut punktene i koordinatsystemet ved å skrive dem inn slik de står i oppgaveteksten, se punkt
Stigningstallet for linja er -250, se verdi
Oppgave 2
2-2a
For å bestemme forskjellen i prosentpoeng finner jeg differansen mellom prosenttallene
For å bestemme forskjellen i prosent så sammenligner jeg differansen med renten for 3 måneder
Hvis hun binder pengene i ett år er renten 0,25 prosentpoeng og 4,76 % høyere enn hvis hun binder pengene i 3 måneder.
2-2b
Jeg finner rentene ved å gange sparebeløpet med rentesatsen
Renteinntektene er 24 300 kroner hvis hun binder pengene i ett år.
Oppgave 3
2-3a
Jeg beregnet gjennomsnittet og standardavviket til turene til Solveig ved å bruke formlene =gjennomsnitt() og =stdav.p() i Excel. Jeg oppsummerer opplysningene om gjennomsnitt og standardavvik til venninnene i tabellen
| Gjennomsnitt | Standardavvik | Median | |
|---|---|---|---|
| Solveig | 7,15 timer | 2,45 timer | 7,5 timer |
| Miriam | 4,7 timer | 4,2 timer | 4 timer |
Solveig har omtrent 2,5 timer høyere gjennomsnitt enn Miriam. Solveig går derfor oftere turer som er veldig lange (hun har et gjennomsnitt på over 7 timer). Gjennomsnittet og medianen til Solveig er ganske like, det tyder på at det er få ekstreme verdier i datamaterialet.
Solveig har et mye lavere standardavvik enn Miriam, nesten 2 timer eller kun
2-3b
Den kumulative frekvensen for turer på 5 timer er 14, og den kumulative frekvensen for turer på 3 timer er 11. De har ikke gått noen turer sammen på 4 timer.
Siden kumulativ frekvens er summen av alle frekvenser for observasjoner som er mindre eller lik den aktuelle observasjonen, kan vi finne frekvensen for antall turer på 5 timer slik:
Ifølge datamaterialet i starten av oppgaven har Solveig gått 4 turer på 8 timer. Ifølge de kumulative frekvensene i tabellen har de to venninnene vært på
Oppgave 4
2-4a
Vi lar
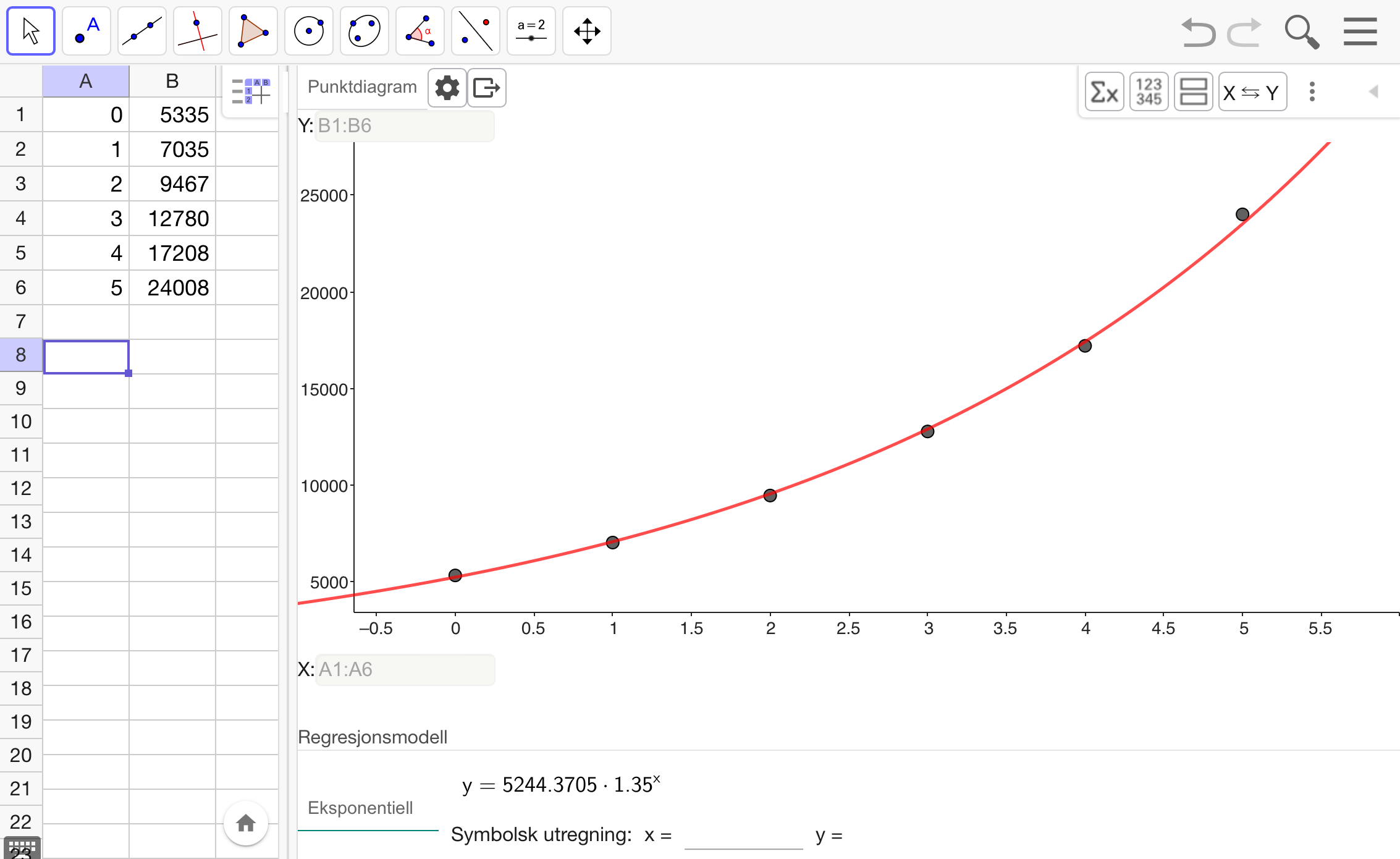
Modellen
2-4b
Tuva har 24 008 følgere i april. Hvis økningen i mai skal være 35 % + 5 prosentpoeng så har hun
I juni øker økningen med enda 5 prosentpoeng til 45 %. Antall følgere i juni vil derfor være
2-4c
Vi kan bruke modellen
Dersom Tuva klarer å holde målet sitt med 5 prosentpoeng økning vil hun i juli ha
Vi finner den prosentvise forskjellen
Tuva vil ha 43,6 % flere følgere i august om hun klarer å nå det nye målet sitt.
Oppgave 5
Påstand 1
Den første søylen i histogrammet har høyde 2 og bredde 40, altså er frekvensen
Påstand 2
Søylen mellom 100 og 150 minutter har høyde 2, altså er frekvensen
Påstand 3
Det er 80 elever som vi kan regne med at har brukt 20 minutter i gjennomsnitt (siden 20 ligger midt i intervallet
Hvis vi fordeler tiden på de 200 elevene får vi gjennomsnittet
Påstand 4
Medianeleven blant de som brukte under 60 minutter er omtrent elev nummer 100. Siden det er 80 elever i det første intervallet, så må vår medianelev være elev nummer 20 av 120 i det andre intervallet. Med andre ord finner vi medianen vår
Medianen vil være 3,33 minutter over bunnen av intervallet vårt, altså ved
Oppgave 6
Thea vil finne beløpet på BSU-kontoen for hvert år hvis hun setter inn 27 500 kr i 10 år fra 2024–2033. Det ser ut til at programmet regner med at hun setter inn pengene i starten av året, og at rentene beregnes ved utgangen av året.
- Linje 1: Setter at innskuddet skal være 27 500 kr
- Linje 2: Setter rentesatsen
- Linje 3: Setter innskuddet til null kroner foreløpig (hun initialiserer variabelen
BSU) - Linje 5: For-løkka kjører 10 ganger. Variabelen
årtar verdiene 2024 til og med 2033. - Linje 7: Hun legger til et nytt innskudd hvert år
- Linje 9: Hun regner ut rentene i kroner
- Linje 11: Hun legger rentene til BSU-kontoen
- Linje 13: Hun skriver ut hvilket år vi er ved utgangen av, hvor mye renteinntekter hun har hatt dette året og det totale beløpet på BSU-kontoen