Løsningsforslag R2 eksamen H2024

Jeg blir veldig glad om du melder ifra om feil enten direkte til meg eller via forumet på matematikk.net.

Oppgave 1-1

1-1a

Siden vi skal regne ut integralet til produktet av to ulike funksjoner vil jeg forsøke delvis integrasjon. Jeg benytter DI-metoden, og velger at $x^{2}$ er den faktoren som skal integreres, og $\ln x$ er faktoren som skal deriveres.

	D	I
+	$\ln x$	$x^{2}$
-	$\frac{1}{x}$	$\frac{1}{3} x^{3}$

Vi kan altså sette opp

\begin{aligned} \int x^{2} \ln x d x & = \ln x \cdot \frac{1}{3} x^{3} - \int \frac{1}{x} \cdot \frac{1}{3} x^{3} d x \\ = \frac{1}{3} x^{3} \ln x - \frac{1}{3} \int x^{2} d x \\ = \frac{1}{3} x^{3} \ln x - \frac{1}{3} \cdot \frac{1}{3} x^{3} + C \\ = \underset{―}{\underset{―}{\frac{1}{3} x^{3} (\ln x - \frac{1}{3}) + C}} \end{aligned}

1-1b

Vi løser først det tilhørende ubestemte integralet ved hjelp av variabelskiftet $u = π t + \frac{π}{4}$ . Da er

\frac{d u}{d t} = π ⟺ d t = \frac{d u}{π}

Vi gjennomfører variabelskiftet

\int \sin (π t + \frac{π}{4}) d t = \int \sin u \frac{d u}{π} = - \frac{1}{π} \cos (u) + C = - \frac{1}{π} \cos (π t + \frac{π}{4}) + C

Vi setter opp det bestemte integralet og setter lik 0.

\begin{aligned} - \frac{1}{π} {[\cos (π t + \frac{π}{4})]}_{0}^{x} & = 0 \\ {[\cos (π t + \frac{π}{4})]}_{0}^{x} & = 0 \\ (\cos (π x + \frac{π}{4})) - (\cos (π \cdot 0 + \frac{π}{4})) & = 0 \\ (\cos (π x + \frac{π}{4})) - (\cos (\frac{π}{4})) & = 0 \\ \cos (π x + \frac{π}{4}) - \cos (\frac{π}{4}) & = 0 \\ \cos (π x + \frac{π}{4}) & = \cos (\frac{π}{4}) \end{aligned}

Vi vet at vi at følgende uttrykk er like

\begin{aligned} (1) \cos (\frac{π}{4}) & = \cos (2 k π + \frac{π}{4}) der k \in Z \\ (2) \cos (\frac{π}{4}) & = \cos (2 k π + \frac{7 π}{4}) der k \in Z \end{aligned}

$x$ er begrenset til intervallet $⟨ 0, π ⟩$ , derfor får vi kun en gyldig løsning fra likning $(1)$

x = 2 k ⟹ x = 2

Fra likning $(2)$ får vi følgende løsning

\begin{aligned} π x + \frac{π}{4} & = 2 k π + \frac{7 π}{4} \\ π x & = 2 π k + \frac{6 π}{4} \\ x & = 2 k + \frac{3}{2} \\ x & = \frac{3}{2} hvis x \in ⟨ 0, π ⟩ \end{aligned}

Løsningene er $\underset{―}{\underset{―}{x = \frac{3}{2}}}$ og $\underset{―}{\underset{―}{x = 2}}$ .

1-1c

Hvis integralet av $\int_{0}^{x} f (t) d t$ skal være lik 0 så må vi ha nøyaktig like mye areal mellom grafen og $x$ -aksen på den positive og negative siden av $x$ -aksen mellom $0$ og $x$ . For en sinusfunksjon så vil vi like mye areal på begge sider av $x$ -aksen når funksjonen har gjennomført et heltall antall perioder fra tiden $t = 0$ .

Oppgave 1-2

1-2a

Summen av en aritmetisk rekke er gitt ved

s_{n} = \frac{a_{1} + a_{n}}{2} \cdot n

Vi ser at differansen $d = 4$ . For å finne ut hvor mange ledd det er i rekka vår kan vi løse

3 + (n - 1) \cdot 4 = 399 ⟹ n - 1 = \frac{399 - 3}{4} ⟹ n = 100

Summen av de 100 første leddene blir altså

s_{100} = \frac{3 + 399}{2} \cdot 100 = \frac{402}{2} \cdot 100 = 201 \cdot 100 = \underset{―}{\underset{―}{20 100}}

1-2b

Vi vet at summen av en uendelig geometrisk rekke som konvergerer er

s = \frac{a_{1}}{1 - k} ⟺ 1 - k = \frac{a_{1}}{s} ⟺ k = 1 - \frac{a_{1}}{s}

Vi setter inn verdiene i uttrykket for $k$

k = 1 - \frac{12}{18} = 1 - \frac{2}{3} = \underset{―}{\underset{―}{\frac{1}{3}}}

1-2c

Vi kan omskrive tallet som sum summen av uendelig rekke med ledd på denne måten $0,757 57575 \dots = 0, 75 + 0,007 5 + 0,000 075 + \dots$

Hvert av disse leddene kan vi skrive om som brøker

\begin{aligned} 0, 75 & = \frac{3}{4} \\ 0,007 5 & = \frac{\frac{3}{4}}{100} = \frac{3}{400} \\ 0,000 075 & = \frac{\frac{3}{4}}{10000} = \frac{3}{40000} \end{aligned}

Vi ser et mønster hvor hvert ledd er $\frac{1}{100}$ av det forrige, altså har vi

\frac{3}{4} + \frac{3}{400} + \frac{3}{40000} + \dots = \frac{3}{4 \cdot 100^{0}} + \frac{3}{4 \cdot 100^{1}} + \frac{3}{4 \cdot 100^{2}} + \dots

Vi har altså vist at $0,757 57575 \dots$ kan skrives som en uendelig geometrisk rekke, og med sumnotasjon blir rekka

lim_{n \to \infty} \sum_{i = 1}^{n} \frac{3}{4 \cdot 100^{i - 1}} = 0,757 57575 \dots

Denne uendelig geometrisk rekka har $a_{1} = \frac{3}{4}$ og $k = \frac{1}{100}$ . Summen av rekka er gitt ved

s = \frac{\frac{3}{4}}{1 - \frac{1}{100}} = \frac{\frac{3}{4}}{\frac{99}{100}} = \frac{300}{396} = \frac{75}{99} = \frac{25}{33}

Siden vi nå vet at $0,757 57575 + \dots = \frac{25}{33}$ så kan vi vise følgende

1,757 57575 \dots = 1 + 0,757 57575 \dots = 1 + \frac{25}{33} = \frac{58}{33}

Vi har altså vist at $1,757 57575 \dots = \frac{58}{33}$ .

Oppgave 1-3

Jeg vet at arealet til et parallellogram utspent av $\vec{a}$ og $\vec{b}$ er gitt ved $| \vec{a} \times \vec{b} |$ , derfor må arealet av bunnen av teltet være gitt ved

A_{△} = \frac{1}{2} | \vec{A B} \times \vec{A C} |

\vec{A B} \times \vec{A C} = | \begin{matrix} {\vec{e}}_{x} & {\vec{e}}_{y} & {\vec{e}}_{z} \\ 3 & 1 & 2 \\ - 1 & 3 & 1 \end{matrix} | = {\vec{e}}_{x} (1 \cdot 1 - 2 \cdot 3) - {\vec{e}}_{y} (3 \cdot 1 - 2 \cdot (- 1)) + {\vec{e}}_{z} (3 \cdot 3 - 1 \cdot (- 1)) = [\begin{matrix} - 5, & - 5, & 10 \end{matrix}]

Arealet er derfor

A_{△} = \frac{1}{2} | \vec{A B} \times \vec{A C} | = \frac{1}{2} \sqrt{(- 5)^{2} + (- 5)^{2} + 10^{2}} = \frac{1}{2} \sqrt{150} = \frac{1}{2} \sqrt{25 \cdot 6} = \frac{1}{2} 5 \cdot \sqrt{6} = \underset{―}{\underset{―}{\frac{5}{2} \sqrt{6}}}

Arealet av bunnen av teltet er $\underset{―}{\underset{―}{\frac{5}{2} \sqrt{6}}}$ .

1-3b

$A$ ligger i origo. Vi vet at lengden av teltstanga $C T$ er $\sqrt{17}$ , og derfor må

\begin{aligned} \sqrt{x^{2} + y^{2} + z^{2}} & = \sqrt{17} \\ \sqrt{t^{2} + t^{2} + (4 t)^{2}} & = \sqrt{17} \\ 18 t^{2} & = 17 \\ t^{2} & = \frac{17}{18} \\ t & = \sqrt{\frac{17}{18}} \end{aligned}

Oppgave 1-4

1-4a

Vi tar utgangspunkt i en sirkel med radius $r = 1$ og legger toppunktet til en vinkel $θ$ i sentrum av sirkelen. Vinkelbeina vil skjære sirkelperiferien og avgrense en sirkelbue $b$ .

Det absolutte vinkelmålet er forholdet mellom sirkelbuen $b$ og omkretsen til hele sirkelen.

θ = \frac{b}{2 π r} = \frac{b}{2 π}

Vi kan bruke forholdet mellom et vinkelmål og en hel omdreining for å gjøre om fra grader til radianer. La $θ$ være det absolutte vinkelmålet til $80^{\circ}$ , da er

\frac{θ}{2 π} = \frac{80^{\circ}}{360^{\circ}} ⟺ θ = \frac{160}{360} π ⟺ θ = \frac{4}{9} π

$80^{\circ}$ er $\frac{4}{9} π$ radianer.

1-4b

\sin v = - \frac{1}{4} = \frac{motstående katet}{hypotenus}

Vi vet at hypotenusen i en enhetssirkel er 1, derfor har vi $mk = - \frac{1}{4}$ . Lengden av den siste kateten i en slik trekant må være

hosliggende katet = \sqrt{h^{2} - {mk}^{2}} = \sqrt{1^{2} - {(- \frac{1}{4})}^{2}} = \sqrt{1 - \frac{1}{16}} = \sqrt{\frac{15}{16}}

Vi ser at vinkelen vår må befinne seg i tredje kvadrant siden $v \in [π, \frac{3 π}{2}]$ . Det betyr at $\cos v = - \sqrt{\frac{15}{16}}$ .

$\tan v$ er gitt ved

\tan v = \frac{\sin v}{\cos v} = \frac{- \frac{1}{4}}{- \sqrt{\frac{15}{16}}} = \frac{1}{\sqrt{15}}

\underset{―}{\underset{―}{\cos v = - \sqrt{\frac{15}{16}} og \tan v = \frac{1}{\sqrt{15}}}}

Oppgave 1-5

1-5a

Vi kan omskrive en sinusfunksjon til en cosinusfunksjon ved å endre på faseforksyvningen. Likevektslinje, periode og amplitude vil være lik som for sinusfunksjonen.

Vi ser at $f$ har et bunnpunkt i $(0, - 3)$ . Vi vet at $\cos u$ har bunnpunkt når $u = π$ , så vi kan faseforskyve med $π$

g (x) = 2 \cdot \cos (\frac{π}{4} x + π) - 1

1-5b

Vi vet at $\cos 60 ° = \cos \frac{π}{3} = \frac{1}{2}$ , derfor må $\cos (\frac{π}{3} + 2 k π) = \frac{1}{2} = \cos (\frac{5 π}{3} + 2 k π)$ der $k \in Z$ . Vi kan løse for $x$ i to steg. Først setter vi opp likningen

\frac{π}{3} + 2 k π = \frac{π}{4} x - π ⟺ x = 8 k + \frac{16}{3}

Siden $x$ er begrenset til $[0, 3 π]$ , så er det kun løsningen $x = \frac{16}{3}$ som er gyldig fra denne likningen.

Deretter kan vi sette opp

\frac{5 π}{3} + 2 k π = \frac{π}{4} x - π ⟺ x = 8 k + \frac{32}{3}

På grunn av avgresningen av $x$ , så får vi kun en gyldig løsning hvis vi velger $k = - 1$ .

x = 8 \cdot (- 1) + \frac{32}{3} = \frac{8}{3}

Likningen har løsningene $x = \frac{8}{3}$ og $x = \frac{16}{3}$ .

Oppgave 2-1

Løsning av oppgave 1 del 2 i CAS

2-1a

$z$ -komponenten til $\vec{r} (t)$ gir oss høyden ved tiden $t = 0$

{\vec{r}}_{z} (0) = 6 - 0, 7 \cdot 0 - 4, 9 \cdot 0^{2} = 6

Posisjonen til ballen etter 0,5 s er gitt ved

\vec{r} (0, 5) = [\begin{matrix} 2 \cdot 0, 5, & 4 \cdot 0, 5, & 6 - 0, 7 \cdot 0, 5 - 4, 9 \cdot 0, 5^{2} \end{matrix}] = [\begin{matrix} 1, & 2, & 4,425 \end{matrix}]

Kanten av hustaket er 6 meter over bakken og ballen befinner seg i punktet $(1, 2, 4,425)$ etter 0,5 sekunder.

2-1b

Vi må først finne ut når ballen treffer bakken, altså når ${\vec{r}}_{z} (t) = 0$ , se linje 1 i GeoGebra. Vi kan se bort fra negative løsninger siden denne modellen kun er gyldig etter at ballen har forlatt kanten av taket.

\begin{aligned} {\vec{r}}_{z} (t) & = 0 \\ 6 - 0, 7 t - 4, 9 t^{2} & = 0 \\ t & = 1,037 4 \end{aligned}

Farten til ballen er gitt ved

\vec{v} (t) = \dot{\vec{r}} (t) = [\begin{matrix} 2, & 4, & - 9, 8 t - 0, 7 \end{matrix}]

Jeg tolker oppgaven slik at vi kun er interessert i farten og ikke retningen til ballen i det den treffer bakken. Farten er i så fall gitt ved

| \vec{v} (t) | = \sqrt{2^{2} + 4^{2} + (9, 8 t - 0, 7)^{2}} = \sqrt{(9, 8 t - 0, 7)^{2} + 20}

Farten når ballen treffer bakken vil være (se linje 2 i GeoGebra)

| \vec{v} (1,037 4) | = \sqrt{(9, 8 \cdot 1,037 4 - 0, 7)^{2} + 20} = 10, 5

Farten er $\underset{―}{\underset{―}{10, 5 m/s}}$ når ballen treffer bakken.

2-1c

Vi løser likningen (se linje 3 i GeoGebra)

\sqrt{(9, 8 t - 0, 7)^{2} + 20} = 10 ⟹ t = 0,984

Igjen kan vi se bort fra den negative løsningen.

Farta til ballen er 10 m/s etter 0,98 sekunder.

Oppgave 2-2

2-2a

Jeg vet at summen av en uendelig geometrisk rekke er gitt ved

s = \frac{a_{1}}{1 - k}

dersom $- 1 < k < 1$ .

Hvis vi vi lar $x = \frac{1}{e}$ så vil rekka bli

1 + (\ln \frac{1}{e} - 1) + {(\ln \frac{1}{e} - 1)}^{2} + \dots

La oss se hva $\ln \frac{1}{e} - 1$ blir

\ln \frac{1}{e} - 1 = \ln 1 - \ln e - 1 = 0 - 1 - 1 = - 2

Det første leddet i rekka er $a_{1} = 1$ og det andre leddet er $a_{2} = - 2$ , det vil si at

k = \frac{- 2}{1} = - 2

$k$ ligger ikke i intervallet $⟨ - 1, 1 ⟩$ , og dermed konvergerer ikke rekka.

Påstanden er usann, rekka konvergerer ikke når $x = \frac{1}{e}$ .

2-2b

$f$ og $g$ kommer til å avgrense maksimalt 2 områder siden $f$ er en tredjegradsfunksjon og $g$ er en andregradsfunksjon. For å finne disse to områdene må vi først finne skjæringspunktene mellom grafene.

Bestemmelse av skjæringspunktet mellom funksjoner i CAS

Jeg fant skjæringspunktene i GeoGebra. (Vi ser her at kravet om at $a > - 1$ gjør at vi får reelle løsninger).

La oss undersøke arealet av områdene som er avgrenset. Jeg gjør dette i GeoGebra ved å integrere fra skjæringspunkt til skjæringspunkt ved hjelp av IntegralMellom.

Bestemmelse av arealet mellom grafene

Påstanden stemmer. Vi ser at arealene mellom grafene er like store.

Oppgave 2-4

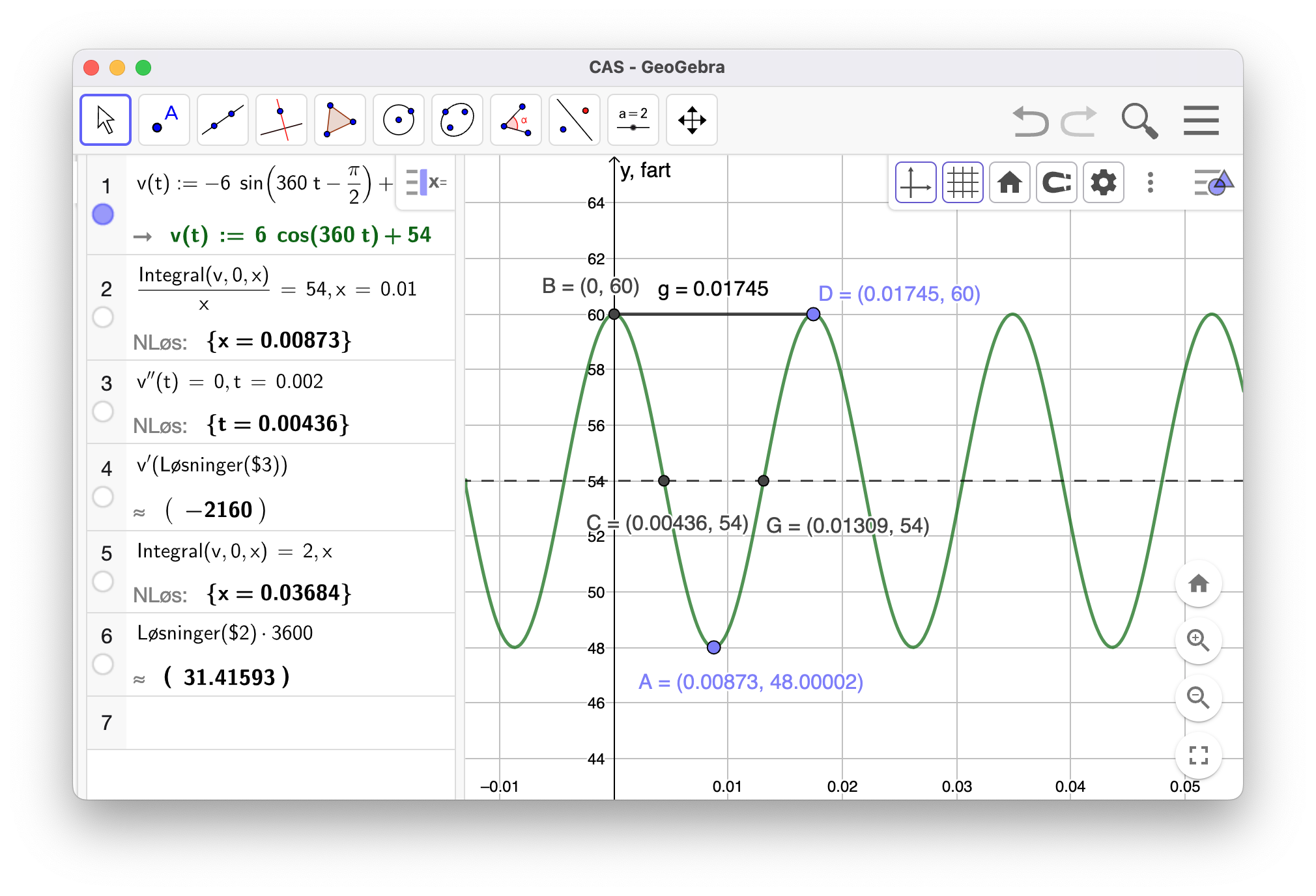
Løsning av oppgave 4 del 2 i CAS

2-4a

Vi ser at likevektslinja er ved 54 km/t, og at sinusfunksjonen har amplituden 6 km/t, samt at den er faseforskjøvet slik vi er allerede har toppfarten 60 km/t ved tiden $t = 0$ . Dermed kan vi konkludere med at gjennomsnittsfarten må være 54 km/t i det vi kommer til fartens første bunnpunkt. Ut fra grafen i GeoGebra ser vi at dette er etter 0,00873 timer.

Vi kan også finne gjennomsnittet av funksjonen slik vi har gjort i linje 2 i CAS i GeoGebra.

Gjennomsnittsfarten var 54 km/t for første gang etter 0,00873 timer eller 31 sekunder.

2-4b

Bilen har størst akselerasjon i vendepunktene. Alle vendepunktene ligger langs likevektslinja $y = 54$ , og vi kan også finne dem ved å løse $v^{″} (t) = 54$ , se linje 3 i CAS.

Perioden til funksjonen er 0,01745 timer eller 63 sekunder, se linja mellom $B$ og $D$ i figuren.

Akselerasjonen har sin største negative verdi etter 0,00436 timer eller 16 sekunder, og deretter hvert 63 sekund etter dette. Se punkt $C$ i figuren.

Akselerasjonen har sin største positive verdi etter 0,01309 timer eller 47 sekunder, og deretter hvert 63 sekund etter dette. Se punkt $D$ i figuren.

2-4c

Vi kan sette opp likningen (se linje 5 i CAS)

\int_{0}^{x} v (t) d t = 2 ⟹ x = 0,036 84

Anders og Ivana må kjøre i 0,03684 timer eller ca 2,21 minutter for å komme til garasjen.

Oppgave 2-5

2-5a

Jeg setter opp tallene i følgen og sjekker differansene mellom hvert ledd (det er alltid et godt tips for å finne mønstre!). Jeg fant ut at differansene mellom tallene var 1, 4, 9, 16, 25, og disse tallene kjenner jeg igjen som kvadrattallene.

Jeg sjekker om jeg finner en god sammenheng for et av leddene

a_{5} = 31 = 15 + 16 = 15 + 4^{2} = a_{4} + 4^{2}

Jeg ser at jeg kan generalisere denne sammenhengen som

\underset{―}{\underset{―}{a_{n + 1} = a_{n} + n^{2}}}

Det finnes også andre sammenhenger som den ekvivalente sammenhengen $a_{n} = a_{n - 1} + (n - 1)^{2}$ eller en sammenheng som ikke bruker $n$ : $a_{n} = {(\sqrt{a_{n - 1} - a_{n - 2}} + 1)}^{2} + a_{n - 1}$ .

2-5b

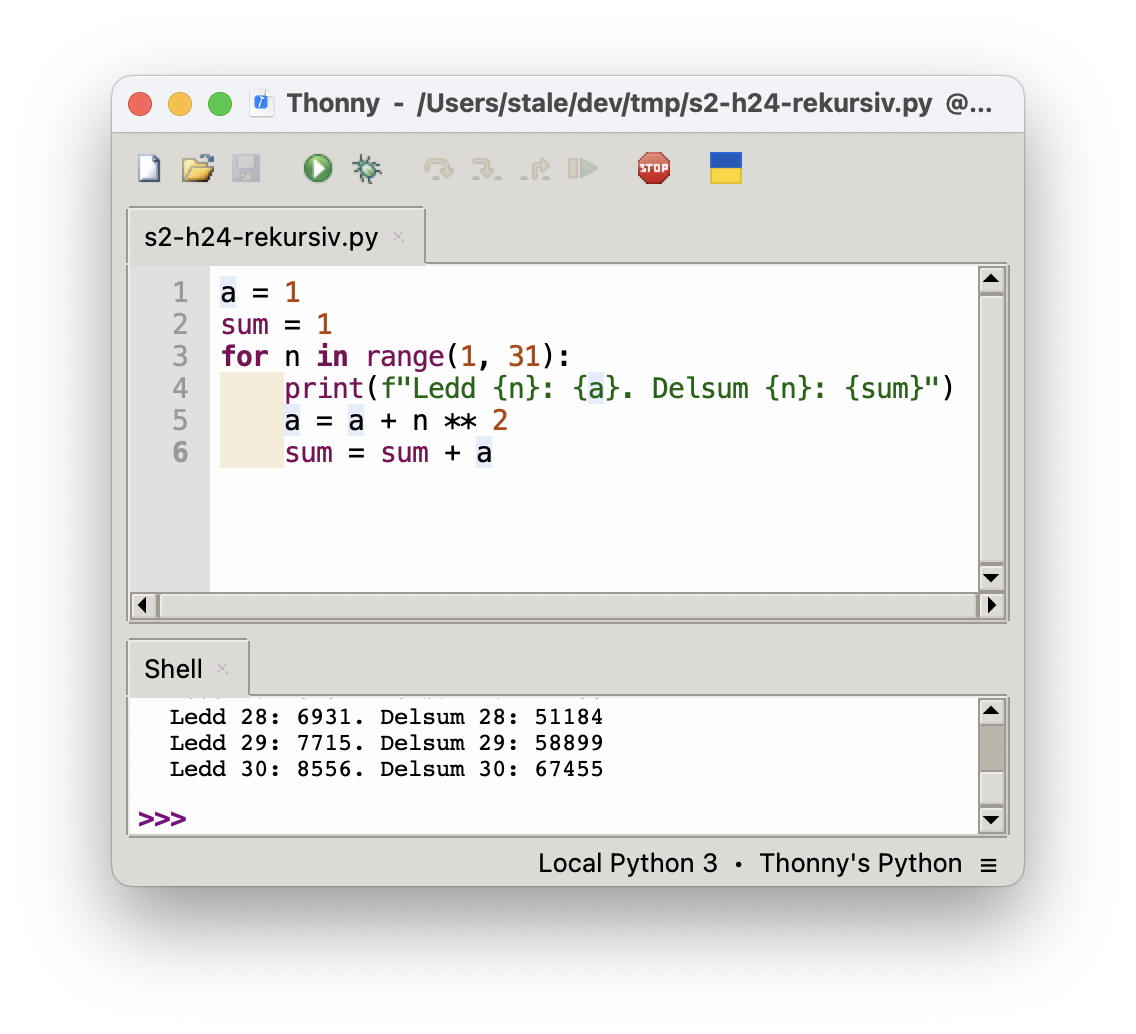
Program for å regne ut ledd i rekke

Jeg brukte en for-løkke til å regne meg fram til ledd nummer 30 og skrev ut svarene i konsollen. Ledd nummer 30 er 8556.

Ulike løsninger på denne oppgaven

Det finnes mange ulike løsninger på denne oppgaven – det viktigste er å passe på at ledd nr. 1 faktisk blir 1, ledd nr. 2 blir 2, ledd nr. 3 blir 6 og så videre. Derfor er det lurt å skrive ut alle leddene, og sjekke at de første leddene blir riktige sammelignet med oppgaveteksten.

Oppgave 2-6

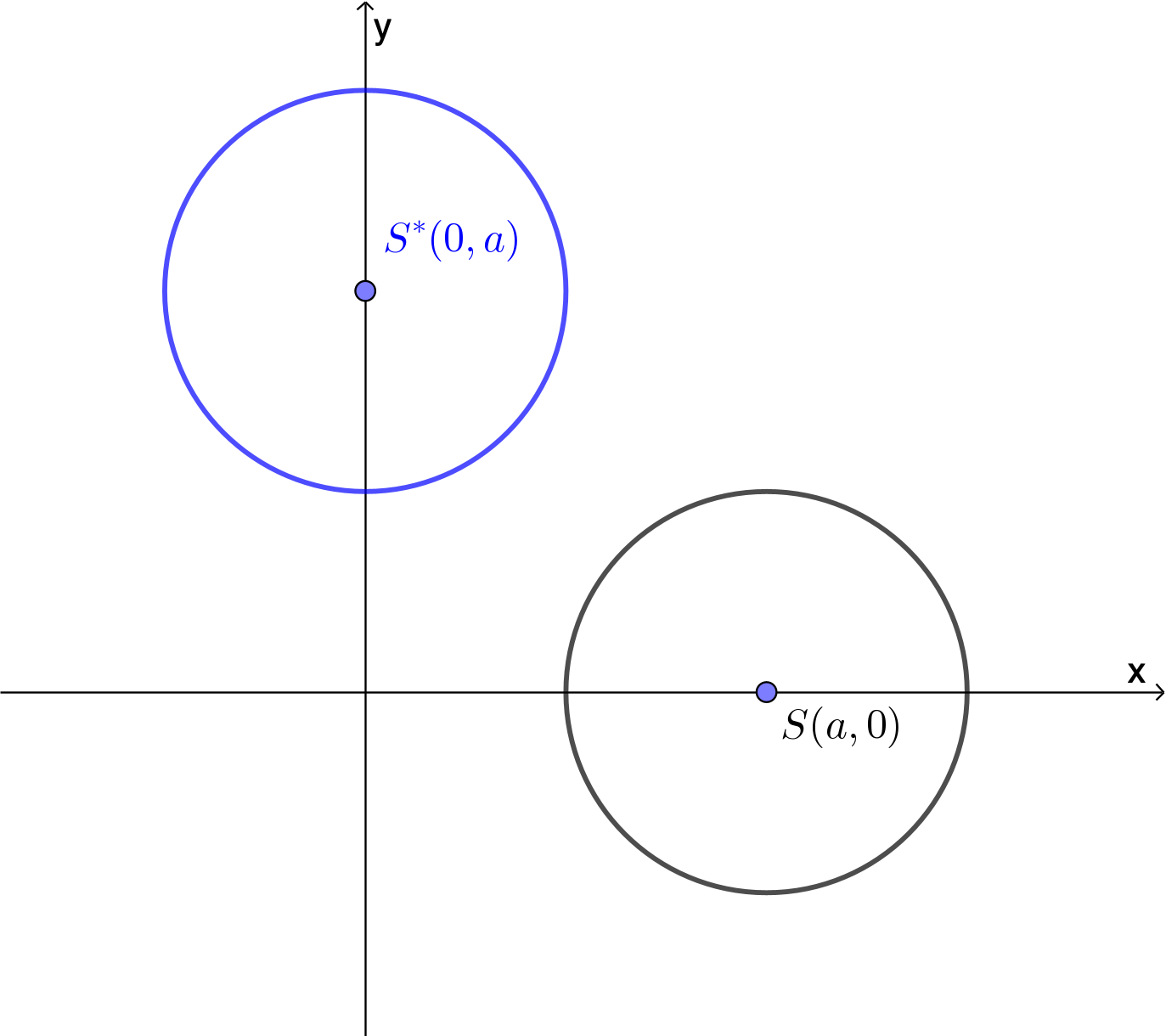
Flytting av sirkelen i oppgave 6

For å gjøre jobben enklere for meg selv så vil jeg flytte sirkelen fra $S (a, 0)$ til $S^{*} (0, a)$ og rotere sirkelen om $x$ -aksen istedenfor om $y$ -aksen. Sirkelens radius er fremdeles $R < a$ .

En sirkel har likningen $x^{2} + y^{2} = R^{2}$ , eller omskrevet for $y$ får vi

y = \pm \sqrt{R^{2} - x^{2}}

Der den positive løsningen vil gi oss den øvre halvsirkelen, og den negative løsningen gir oss den nedre halvsirkelen.

Vår sirkel er forskjøvet med $a$ enheter i positiv $y$ -retning, derfor er uttrykket for sirkelen vår

y = \pm \sqrt{R^{2} - x^{2}} + a

Vi kan bruke formelen for omdreiningslegeme for å finne volumet. Vi bruker først formelen for den øvre halvsirkelen og finner dermed volumet av en slags smultring uten hull. Deretter lager vi et hull i smultringen ved å trekke fra volumet av omdreiningslegemet definert av den nedre halvsirkelen.

Formelen for 360º omdreining rundt $x$ -aksen er

V = π \int_{a}^{b} {(f (x))}^{2} d x

Grensene for integrasjonen er $x = - R$ og $x = R$ .

$R$ er positiv, så vi har $sgn (R) = 1$ i vårt tilfelle (se faktaboks lenger nede for mer info).

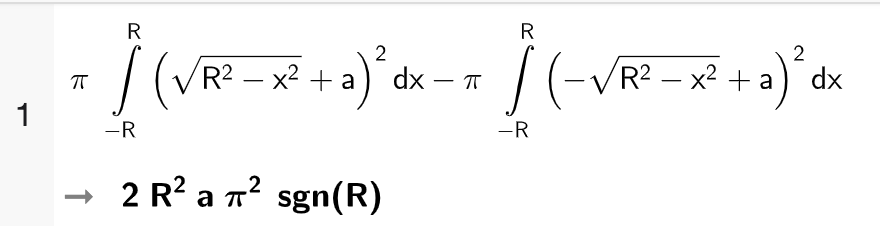
Volumet av omdreiningslegemet er $2 π^{2} R^{2} a$ , som skulle vises.

sgn-funksjonen

GeoGebra gir oss en litt ukjent sgn(R)-funksjon i tillegg til uttrykket vi skulle finne. sgn()-funksjonen er definert slik >

sgn (x) = {\begin{cases} 1 & hvis x > 0 \\ 0 & hvis x = 0 \\ - 1 & hvis x < 0 \end{cases}

Hvis du møter på slike ukjente funksjoner på eksamen, prøv å skrive inn sgn(2) og sgn(-5) i GeoGebra og sjekk hva du får som svar, eller forsøk å tegne funksjonen.