Løsningsforslag S1 eksamen V2023

Oppgave 1-1

\frac{{(2 a b^{- 1})}^{3} \cdot {(a^{2} b^{- 2})}^{- 1}}{4 a^{2} b^{- 3}} = \frac{2^{3} a^{3} b^{- 1 \cdot 3} a^{2 \cdot (- 1)} b^{(- 2) \cdot (- 1)} a^{- 2} b^{3}}{4} = \frac{8}{4} \cdot a^{(3 - 2 - 2)} \cdot b^{(- 3 + 2 + 3)} = \underset{―}{\underset{―}{\frac{2 b^{2}}{a}}}

Oppgave 1-2

Bruker produktregelen med $u = x, v = \ln x$ .

f^{'} (x) = (u^{'} \cdot v + u \cdot v^{'}) = 1 \cdot \ln x + {x \cdot \frac{1}{x}}^{1} = \underset{―}{\underset{―}{\ln x + 1}}

Oppgave 1-3

Ser at både teller og nevner går mot null når $x \to 2$ . Vi kan derfor bruke L'Hopitals regel.

lim_{x \to 2} \frac{f (x)}{g (x)} = lim_{x \to 2} \frac{f^{'} (x)}{g^{'} (x)} = lim_{x \to 2} \frac{3 x^{2}}{2 x} = lim_{x \to 2} \frac{3 x}{2} = \frac{3 \cdot 2}{2} = \underset{―}{\underset{―}{3}}

Oppgave 1-4

1-4a

Dette er et hypergeometrisk forsøk siden vi har to typer objekter og skal trekke $k_{1} = 2$ av den ene typen og $k_{2} = 1$ av den andre typen

\frac{(\binom{n_{1}}{k_{1}}) (\binom{n_{2}}{k_{2}})}{(\binom{n}{k})} = \frac{(\binom{3}{2}) (\binom{4}{1})}{(\binom{7}{3})} = \frac{\frac{3!}{2! \cdot 1!} \cdot 4}{\frac{7!}{3! \cdot 4!}} = \frac{3 \cdot 4}{\frac{7 \cdot 6 \cdot 5}{3 \cdot 2}} = \frac{12 \cdot 3 \cdot 2}{210} = \frac{72}{210} = \frac{12}{35}

1-4b

La $X$ være antall hvite kuler. Da er

P (X \geq 2) = 1 - P (X \leq 1) = 1 - (P (X = 1) + P (X = 0))

Vi har allerede bestemt sannsynligheten for $P (X = 1) = \frac{12}{35}$ i oppgave a).

P (X = 0) = \frac{3}{7} \cdot \frac{2}{6} \cdot \frac{1}{5} = \frac{3 \cdot 2}{7 \cdot 6 \cdot 5} = \frac{6}{210} = \frac{1}{35}

P (X \geq 2) = 1 - (\frac{12}{35} + \frac{1}{35}) = 1 - \frac{13}{35} = \underset{―}{\underset{―}{\frac{22}{35}}}

Oppgave 1-5

Programmet regner ut en tilnærmingsverdi for den deriverte av $K (x) = 0, 2 x^{2} + 140 x + 7000$ i punktet $x$ helt fram til den deriverte når verdien 260.

Vi kan løse denne oppgaven for hånd ved å derivere $K$ og sette svaret lik 260.

\begin{aligned} K^{'} (x) & = 0, 4 x + 140 \\ 260 & = 0, 4 x + 140 \\ 120 & = 0, 4 x \\ x & = \frac{120}{0, 4} \\ x & = 300 \end{aligned}

Svaret fra programmet blir 300. Svaret forteller bedriften at ved produksjon av 300 enheter så stiger kostnadene med 260 kroner per enhet.

\clearpage

Oppgave 2-1

2-1a

Timelønna har vokst med $340, 10 - 272, 55 = 67, 55$ kr i løpet av disse 14 årene. Vi kan sette opp dette uttrykket for å bestemme vekstfaktoren $x$

\begin{aligned} 272, 55 \cdot x^{14} & = 340, 10 \\ x & = \sqrt[14]{\frac{340, 10}{272, 55}} \\ x & = 1,015 94 \end{aligned}

Den gjennomsnittlige årlige prosentvise økninga har vært 1,59 %.

2-1b

Jeg brukte regresjon i GeoGebra og fant at en god eksponentialmodell for lønnsveksten er

g (x) = 277, 8 \cdot 1,015 5^{x}

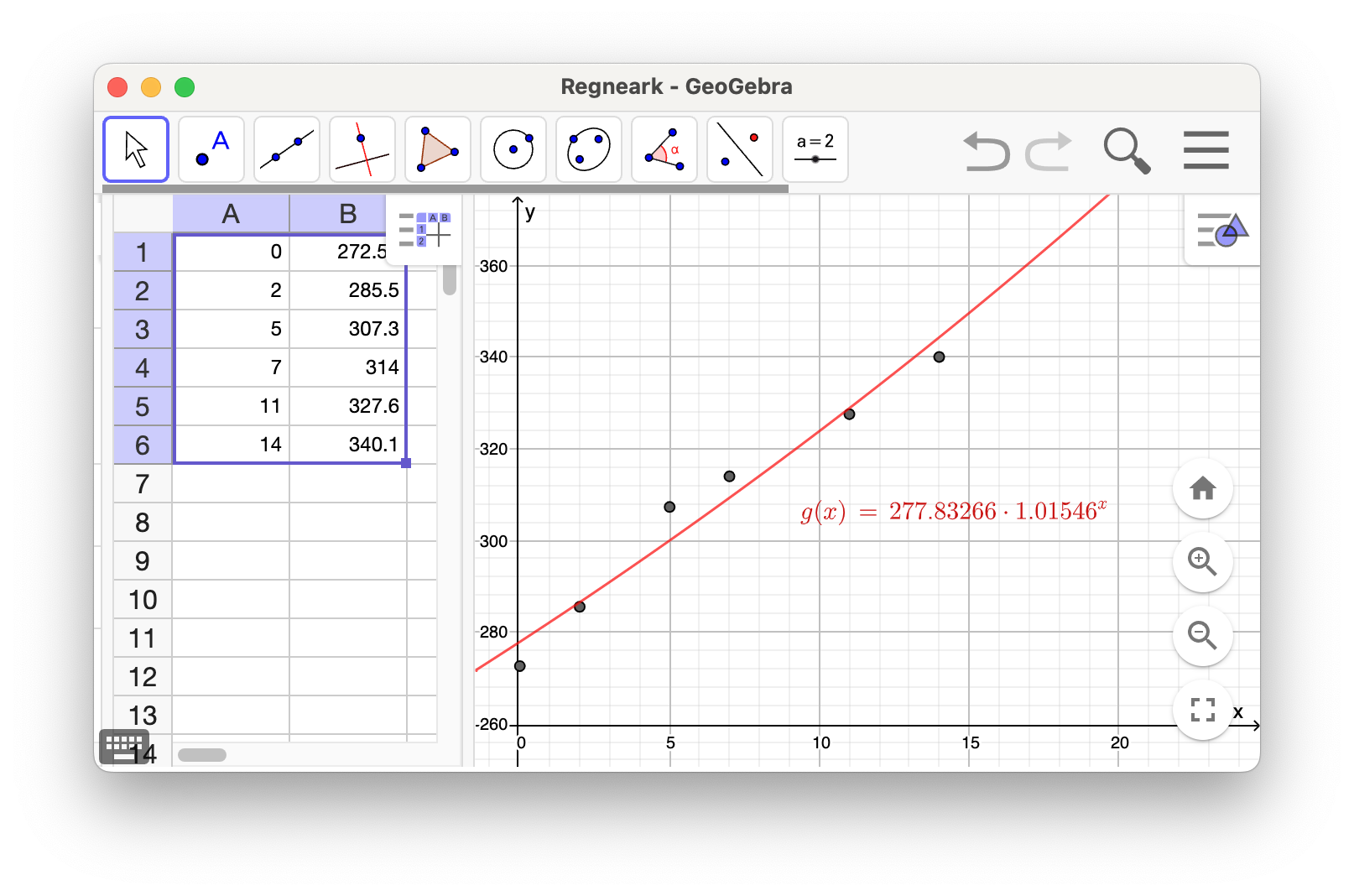
2-1c

Hvis man skal regne Per sin lønn riktig så må man egentlig vite lønna hvert år og summere opp årslønnene som ei rekke. Jeg bruker heller modell $g$ som en tilnærming til Pers lønn.

For min del er det raskest å legge inn formelen =272,55*1,023^(2008-A2)*1700 i cellene til Amalie for å regne ut hennes lønn, og tilsvarende for Per.

År	Per	Amalie
2008	kr 472 260,00	kr 463 335,00
2009	kr 479 580,03	kr 473 991,71
2010	kr 487 013,52	kr 484 893,51
2011	kr 494 562,23	kr 496 046,07
2012	kr 502 227,94	kr 507 455,12
2013	kr 510 012,48	kr 519 126,59
2014	kr 517 917,67	kr 531 066,50
2015	kr 525 945,40	kr 543 281,03
2016	kr 534 097,55	kr 555 776,50
2017	kr 542 376,06	kr 568 559,36
2018	kr 550 782,89	kr 581 636,22
2019	kr 559 320,02	kr 595 013,86
2020	kr 567 989,48	kr 608 699,17
2021	kr 576 793,32	kr 622 699,25
2022	kr 585 733,62	kr 637 021,34
Sum	kr 7 906 612,22	kr 8 188 601,24

Amalies samlede lønn er omtrent 8 188 600 kr i perioden. Pers samlede lønn er omtrent 7 906 600 kr.

2-1d

Igjen så er det enklest og raskest for meg å bruke målsøking i Excel for å løse oppgaver som dette. Jeg lager en celle med vekstfaktoren til Per og målsøker slik at lønna i 2022 skal bli lik for begge.

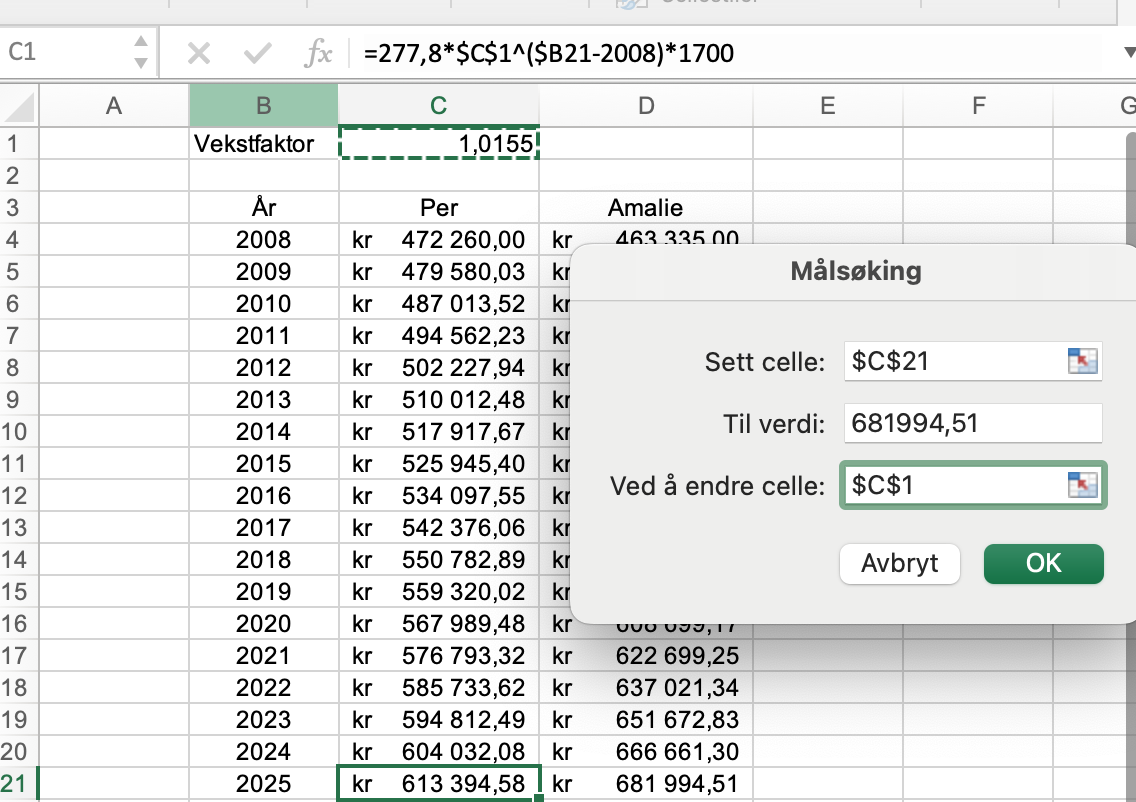
Vekstfaktoren ble endret til 1,02185.

Lønnen til Per må stige med omtrent 2,185 % hvert år for at de skal ha lik lønn i 2025.

Oppgave 2-2

2-2a

Kommentar

Det er enklest å vise dette ved å tegne opp grafene til $(\ln x)^{4}$ og $4 \ln x$ . Da ser man at disse uttrykkene ikke er like unntatt for $x = 1 \lor x = e^{\sqrt[3]{4}}$ . Det er også mulig å løse oppgaven ved å argumentere med tekst slik som jeg har gjort nedenfor.

$(\ln x)^{4}$ er det samme som $\ln x \cdot \ln x \cdot \ln x \cdot \ln x$ , og dette er ikke nødvendigvis det samme som $4 \ln x$ . Som et konkret moteksempel lar vi $x = e$ .

(\ln x)^{4} = (\ln e)^{4} = 1^{4} = 1

Hvis vi sjekker $4 \ln x$ får vi

4 \ln x = 4 \ln e = 4 \cdot 1 = 4

$(\ln x)^{4} \neq 4 \ln x$ . Påstanden er ikke riktig.

2-2b

En fjerdegradsfunksjon $f (x) = a x^{4} + b x^{3} + c x^{2} + d x + e$ har minst ett stasjonært dersom $f^{'} (x) = 4 a x^{3} + 3 b x^{2} + 2 c x + d$ har minst ett nullpunkt.

Tredjegradsfunksjonen $f^{'}$ vil alltid ha minst ett nullpunkt. $f^{'}$ vil oppføre seg på en av to måter

$lim_{x \to \infty} f^{'} (x) = \infty \land lim_{x \to - \infty} f^{'} (x) = - \infty$ . $f^{'}$ vil altså gå fra $- \infty$ mot $+ \infty$ når $x$ vokser.
$lim_{x \to \infty} f^{'} (x) = - \infty \land lim_{x \to - \infty} f^{'} (x) = \infty$ . $f^{'}$ vil altså bevege seg fra $+ \infty$ mot $- \infty$ når $x$ vokser.

Siden $f^{'}$ må krysse $x$ -aksen så må det stasjonære punktet være enten et toppunkt eller et bunnpunkt.

En fjerdegradsfunksjon har alltid minst ett toppunkt eller bunnpunkt.

2-2c

La den stokastiske variabelen $X_{1}$ være resultatet av første trekning fra de 34 tallene. Sannsynligheten for hvert tall er like stor. Det er 17 tall som er mindre enn 18, altså

P (X_{1} < 18) = \frac{17}{34} = \frac{1}{2}

La den stokastiske variabelen $X_{2}$ være resultatet av andre trekning fra de 33 tallene. $P (X_{2} < 18) = \frac{16}{33}$ . For hvert tall vi trekker vil tallene i teller og nevner reduseres med 1.

Vi får det samme mønsteret for at ingen tall er mindre enn 18.
Sannsynligheten for tallet ikke er mindre enn 18 er gitt ved

\begin{aligned} P (X_{1} \geq 18) & = \frac{17}{34} = \frac{1}{2} \\ P (X_{2} \geq 18) & = \frac{16}{33} \end{aligned}

Mønsterne vil utvikle seg på samme måte.

Det er like sannsynlig at alle lottotallene er mindre enn 18 som at ingen av lottotallene er mindre enn 18.

Oppgave 2-3

2-3a

Programmet har to nøstede for-løkker. $i$ og $j$ er antall øyne på to terninger. Den første løkka lar $i$ være et tall fra 1 til 6 (matematisk ${i ∣ i \in N, i < 6}$ ). Den andre løkka gjør det samme for $j$ . Den innerste koden med if-setningen vil kjøres $6 \cdot 6 = 36$ ganger, én gang for hver kombinasjon av $i$ og $j$ .

if setningen sjekker om summen av terningene er over 8, i så fall så legger vi til én på antall gunstige utfall. Til slutt finner vi sannsynligheten ved $\frac{gunstige utfall}{mulige utfall}$ .

Mona prøver å finne sannsynligheten for at summen av to terninger blir større eller lik 8.

2-3b

Bruker programmet som Mona har skrevet, men legger til en ekstra terning og endrer på vilkåret i if-setningen. For å sjekke om ett av flere vilkår er sanne bruker jeg or. Antall mulige utfall er nå $6^{3} = 216$ .

g = 0
for i in range(1, 7):
	for j in range(1, 7):
		for k in range(1, 7):
			if (i+j+k == 7) or (i+j+k == 11):
				g = g + 1

print(g/6**3)

Output: 0.19444444444444445

Sannsynligheten for å få 7 eller 11 er 0,194.

Oppgave 4

2-4a

La $I (x)$ være inntektsfunksjon, $p$ være pris og $x = e (p)$ være antall solgte enheter. Da er

I (x) = p \cdot x = p \cdot e (p)

Regner ut inntektene for prisen 40 kroner

I (40) = 40 \cdot e (40) = 40 \cdot 2100 = 84000

De daglige inntektene er 84 000 kr ved prisen 40 kr.

2-4b

Lager et funksjonsuttrykk for $e (p)$ ved å lese av grafen. Ser at konstantleddet er 4500 og stigningstallet er $\frac{1500 - 4500}{50} = - 60$ . Det gir

e (p) = - 60 p + 4500

Setter opp uttrykket for inntektene og setter lik 75 000 kr og løser i CAS.

\begin{aligned} I (p) & = p \cdot e (p) \\ 75 000 & = p \cdot (- 60 p + 4500) \\ - 60 p^{2} + 4500 p - 75000 & = 0 \\ p = 25 & \lor p = 50 \end{aligned}

Prisen må være 25 kr eller 50 kr for at de daglige inntektene skal bli 75 000 kr.

2-4c

Inntektene er størst i toppunktet til $I$ . Det er enklest å løse denne ved å tegne $I (p) = - 60 p^{2} + 4500 p$ i GeoGebra og finne toppunktet, men vi kan også gjøre dette ved regning.

$I$ må være ved et topp- eller bunnpunkt ved $I^{'} (p) = 0$ . Siden det er negativ koeffisient foran $p^{2}$ -leddet har andregradsfunksjonen et toppunkt.

\begin{aligned} I^{'} (p) & = - 2 \cdot 60 p + 4500 \\ 0 & = - 120 p + 4500 \\ 120 p & = 4500 \\ p & = 37, 5 \end{aligned}

Vi får størst daglige inntekter ved prisen 37,5 kr per enhet.

Oppgave 2-5

2-5a

Vi kan regne med en binomisk sannsynlighetsfordeling her med $n = 1300$ og $p = 0, 45$ siden

billettmottakerne har to muligheter: de kommer på kamp, eller de kommer ikke på kamp
det er samme sannsynlighet for hver billettmottaker
så lenge billettmottakerne er uavhengige av hverandre (hvis de 1300 billettene deles ut i stor by stemmer sikkert dette, men hvis det er på en veldig liten plass så er nok ikke billettmottakerne egentlig uavhengige av hverandre)

Denne løses enklest i sannsynlighetskalkulatoren i GeoGebra, eller ved et enkelt program:

from scipy.stats import binom
P = 1-binom.cdf(599,1300,0.45)      # 1 - sannsynlighet for 
									# at opptil 599 kommer
print(f"P(X >= 600) = {P:.4f}")

output: P(X >= 600) = 0.2094

Sannsynligheten for at minst 600 mennesker kommer er 20,9 %.

2-5b

from scipy.stats import binom
n = 1299
P = 0
while P < 0.95:
    n = n + 1
    P = 1-binom.cdf(599,n,0.45)
print(f"Ved n = {n} er P(X >= 600) = {P:.4f}.")

output: Ved n = 1401 er P(X >= 600) = 0.9519

Siden jeg allerede var igang med programmering så programmerte jeg denne også. Du kan også finne sannsynlighetene i Excel ved å lage et regneark på denne formen:

Rad/Kol	A	B
1	Antall, $n$	$P (X \leq n)$
2	1300	`=BINOM.FORDELING.N(599;A2;0,45;SANN)`

Oppgave 2-6

2-6a

\begin{aligned} 130 & = 120 + 10 \log I \\ 10 \log I & = 130 - 120 \\ \log I & = {\frac{10}{10}}^{1} \\ 10^{\log I} & = 10^{1} \\ I & = 10 \end{aligned}

Lydintensiteten er 10 W/m² når lydstyrken er 130 dB.

2-6b

Når $L = 132$ blir

I = 10^{\frac{132 - 120}{10}} = 10^{1, 2} = 15, 85

Økningen i prosent er

\frac{15, 85 - 10}{10} = 0,585 = 58, 5 %

Når lydstyrken øker fra 130 dB til 132 dB øker lydintensiteten med 58,5 %.

2-6c

Vi vet at $L = 140$ når $r = 50$ . Jeg løser for $E$ og finner (dette gjøres enklest i CAS)

\begin{aligned} L & = 120 + 10 \log I \\ L & = 120 + 10 \log \frac{E}{4 π r^{2}} \\ 140 & = 120 + 10 \log \frac{E}{4 π 50^{2}} \\ E & = 1000000 π \end{aligned}

Jeg tolker formlene slik at et fly lager lyd med effekten $E = 1 000 000 π W$ , mens lydintensiteten og lydstyrken avtar med avstanden. Vi setter opp en likning med lydstyrke lik 130 dB og finner avstanden som kreves (dette gjøres også enklest i CAS).

\begin{aligned} 130 & = 120 + 10 \log \frac{1000000 π}{4 π r^{2}} \\ 10 & = 10 \log \frac{1000000}{4 r^{2}} \\ 1 & = \log \frac{250000}{r^{2}} \\ 10 & = \frac{250000}{r^{2}} \\ r^{2} & = \frac{250000}{10} \\ r^{2} & = 25000 \\ r & = | 158,113 | \end{aligned}

Ved 158,113 m så er altså lydstyrken 130 dB. Siden vi skulle finne den minste avstanden hvor lydstyrken var lavere enn 130 dB så runder jeg opp i svaret mitt.

158,12 m fra flyet er den minste avstanden hvor lydstyrken er lavere enn 130 dB.