Løsningsforslag S2 eksamen V2024

Jeg blir veldig glad om du melder ifra om feil enten direkte til meg eller via forumet på matematikk.net.

Oppgave 1-1

1-1a

\begin{aligned} \int_{- 1}^{0} (- x^{3} + 3 x) d x \\ {[- \frac{1}{4} x^{4} + \frac{3}{2} x^{2}]}_{- 1}^{0} \\ 0 - (- \frac{1}{4} (- 1)^{4} + \frac{3}{2} (- 1)^{2}) \\ - (- \frac{1}{4} + \frac{3}{2}) & = - \frac{5}{4} \end{aligned}

Integralet er $\underset{―}{\underset{―}{- \frac{5}{4}}}$ .

1-1b

Jeg finner først nullpunktene ved å faktorisere uttrykket.

f (x) = - x^{3} + 3 x = - x (x^{2} - 3) = - x (x^{2} - {(\sqrt{3})}^{2}) = - x (x + \sqrt{3}) (x - \sqrt{3})

Vi har nullpunkter når $f (x) = 0$ . Det vil si at vi har nullpunkter når $x = - \sqrt{3}, x = 0, x = \sqrt{3}$ . Det er kun nullpunktet $x = 0$ som ligger mellom $x = - 1$ og $x = 1$ .

For å finne ut om funksjonen er positiv eller negativ i intervallene så sjekker jeg funksjonsverdien i $x = - 1$ og $x = 1$ .

f (- 1) = - (- 1)^{3} + 3 (- 1) = 1 - 3 = - 2

f (1) = - (1)^{3} + 3 \cdot 1 = - 1 + 3 = 2

Alternativ måte å sjekke hvor funksjonen er positiv og negativ

Siden integralet $\int_{- 1}^{0} f (x) d < 0$ og det ikke finnes noen nullpunkter for $x \in ⟨ - 1, 0 ⟩$ , så må $f$ være negativ når $x \in ⟨ - 1, 0 ⟩$

$f$ er altså negativ i intervallet $[- 1, 0 ⟩$ og positiv i intervallet $⟨ 0, 1]$ . Vi finner arealet ved å ta integralene av hver del (og husker minustegn foran integralet til området som ligger under $x$ -aksen).

\begin{aligned} A & = - \int_{- 1}^{0} f (x) d x + \int_{0}^{1} f (x) d x \\ A & = - (- \frac{5}{4}) + {[- \frac{1}{4} x^{4} + \frac{3}{2} x^{2}]}_{0}^{1} \\ A & = \frac{5}{4} + - \frac{1}{4} + \frac{3}{2} = \frac{10}{4} = \frac{5}{2} \end{aligned}

Arealet av området er $\underset{―}{\underset{―}{\frac{5}{2}}}$ .

Antisymmetri

Du kan utnytte antisymmetrien til $f$ til å argumentere for at arealet avgrenset av $x = - 1$ , $f$ , $x$ -aksen og $x = 0$ vil være like stort som arealet avgrenset av $f$ , $x$ -aksen, $x = 0$ og $x = 1$ .

Oppgave 1-2

1-2

Jeg ser at hvis jeg velger $u = x^{2} + 1$ og bruker variabelskifte, så kan jeg forkorte bort $2 x$ -faktoren senere.

\begin{aligned} \int (x^{2} + 1)^{3} \cdot 2 x d x & = \int u \cdot 2 x d x \\ u & = x^{2} + 1 \\ \frac{d u}{d x} & = 2 x \\ d x & = \frac{d u}{2 x} \end{aligned}

Jeg erstatter $d x$ i det opprinnelige integralet med $\frac{d u}{2 x}$

\int u^{3} \cdot 2 x d x = \int u^{3} \cdot 2 x \frac{d u}{2 x} = \int u^{3} d u = \frac{1}{4} u^{4} + C = \underset{―}{\underset{―}{\frac{1}{4} (x^{2} + 1)^{4} + C}}

Oppgave 1-3

1-3a

Programmet viser en aritmetisk følge hvor hvert ledd er gitt av $a_{n} = 4 n - 2$ for $n > 0$ . Programmet regner ut delsummene, $S_{n}$ , til den tilhørende rekka.

Programmet finner ut hvilket ledd i rekka som gjør at delsummen blir over 200.

1-3b

Siden tallfølgen er aritmetisk kan vi regne ut summen av de $n$ første leddene med

S_{n} = \frac{a_{1} + a_{n}}{2} n

Jeg vet at summen skal være over 200, at $a_{1} = 2$ og jeg kan erstatte $a_{n}$ med $4 n - 2$ . Dette gir

\begin{aligned} 200 & = \frac{2 + 4 n - 2}{2} n \\ 200 & = 2 n^{2} \\ 100 & = n^{2} \\ 10 & = n \end{aligned}

$n = 10$ gir oss altså nøyaktig delsummen $S_{10} = 200$ . $n = 11$ gir oss den første delsummen som er over 200.

Programmet skriver ut 11.

Oppgave 1-4

1-4a

La $X$ være vekten til en tilfeldig valgt fisk. Da er forventningsverdien $E (X) = 4700$ .

Vi vet at 88,5 % av fisken som slaktes veier mindre eller lik 5300 gram. Ifølge normalfordelingstabellen så er $0,885 = Φ (1, 2) ⟹ z = 1, 2$ .

Vi kan da sette opp likningen

z = \frac{x - μ}{σ} ⟺ 1, 2 = \frac{5300 - 4700}{σ} ⟺ σ = \frac{600}{1, 2} = 500

Standardavviket for en vilkårlig valgt laks er 500 gram.

1-4b

Vi gjør om til standard normalfordeling

z = \frac{4500 - 4700}{500} = - \frac{200}{500} = - 0, 4

Normalfordelingstabellen gir oss $Φ (- 0, 4) = 0,345$ .

Sannsynligheten for at en vilkårlig valgt laks veier mindre enn 4500 gram er 34,5 %.

Oppgave 1-5

Vi har de laveste enhetskostnadene når $E^{'} (x) = 0$ . Vi kan altså sette opp

\begin{aligned} E^{'} (x) & = 0 \\ {(\frac{K (x)}{x})}^{'} & = 0 \\ \frac{K^{'} (x) \cdot x - K (x) \cdot 1}{x^{2}} & = 0 \\ K^{'} (x) \cdot x - K (x) & = 0 \\ K^{'} (x) & = \frac{K (x)}{x} \\ K^{'} (x) & = E (x) \end{aligned}

Hvis $x_{0}$ er antallet enheter som gir lavest enhetskostnader så ser vi at dette må være lik grensekostnaden, altså $K^{'} (x_{0}) = E (x_{0})$ .

Oppgave 1-6

1-6a

For å finne forventningsverdien lager jeg en tabell og regner ut $\sum_{i = 1}^{6} x \cdot P (X = x)$

$x$	$P (X = x)$	$x \cdot P (X = x)$
1	$\frac{1}{6}$	$1 \cdot \frac{1}{6} = \frac{1}{6}$
2	$\frac{1}{6}$	$2 \cdot \frac{1}{6} = \frac{2}{6}$
3	$\frac{1}{6}$	$3 \cdot \frac{1}{6} = \frac{3}{6}$
4	$\frac{1}{6}$	$4 \cdot \frac{1}{6} = \frac{4}{6}$
5	$\frac{1}{6}$	$5 \cdot \frac{1}{6} = \frac{5}{6}$
6	$\frac{1}{6}$	$6 \cdot \frac{1}{6} = \frac{6}{6}$
Sum	1	$\frac{21}{6} = \frac{7}{2} = 3, 5$

Forventningsverdien er 3,5.

1-6b

Standardavviket til ett kast er $S D (X) = 1, 7$ .

Vi lar $S$ være summen av $n$ forsøk med $X$ slik at

S = X_{1} + X_{2} + X_{3} + \dots + X_{n}

Sentralgrensesetningen sier at $S$ vil være tilnærmet normalfordelt med variansen og standardavviket:

Var (S) = n \cdot Var (X) ⟹ S D (S) = \sqrt{n} \cdot S D (X)

Fra normalfordelingstabellen så kan jeg finne ut at 68 % av arealet under normalfordelingskurven ligger innenfor pluss/minus ett standardavvik fra forventningsverdien. Altså må det være 32 % sannsynlighet for å få observasjon mer enn ett standardavvik fra forventningsverdien.

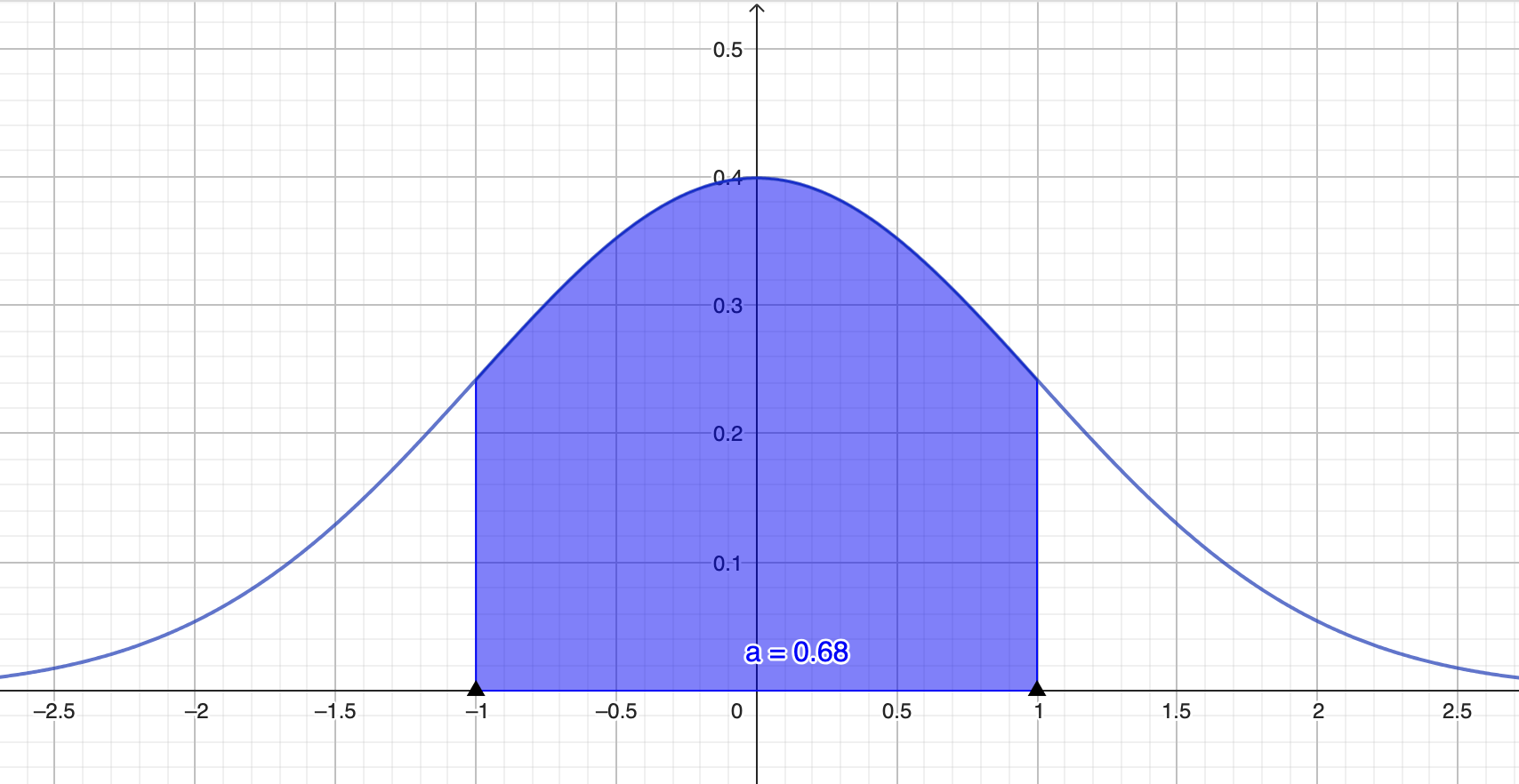
Siden vi vet at 32 % tilsvarer mer enn ett standardavvik fra forventningsverdien, må 17 øyne være ett standardavvik.

\begin{aligned} S D (S) & = 17 \\ \sqrt{n} \cdot S D (X) & = 17 \\ \sqrt{n} \cdot 1, 7 & = 17 \\ \sqrt{n} & = 10 \\ n & = 100 \end{aligned}

Hilde må kaste terningen 100 ganger før det er omtrent 32 % sannsynlighet for at summen av antall øyne er mer enn 17 unna forventningsverdien for summen.

Oppgave 2-1

CAS-utklipp til oppgave 2-1

2-1a

Jeg ser at funksjonen er logistisk og jeg vet at den største vekstfarten er i vendepunktet.

Jeg finner vendepunktet i GeoGebra, se linje 2 i utklippet, vendepunktet er ved 25 enheter solgt. Vekstfarten ved 25 solgte enheter finner jeg ved å bestemme $f^{'} (25)$ i linje 3.

Salget økte raskest i uke 25, da økte salget med 21 enheter per uke.

2-1b

Vi kan finne det samlede salget ved å bestemme arealet under grafen til $f$ .

I linje 4 setter jeg opp likningen

\int_{0}^{x} f (t) d t = 2000

Det tok nesten 19 uker før salget passerte 2000 enheter.

2-1c

Inntektene fra salget må være gitt ved antall enheter solgt $\times$ pris per enhet.

I linje 5 setter jeg opp likningen

\int_{0}^{52} f (t) d t \cdot p = 1 000 000

der $p$ er den ukjente prisen per enhet.

Butikken har solgt produktet for 53 kr.

Oppgave 2-2

2-2a

$X$ er binomisk fordelt fordi

Vi har $n$ delforsøk
Sannsynligheten for at legemiddelet fungerer er $p = 0, 75$ i alle forsøkene
Vi må anta at vi tester legemiddelet på tilfeldige pasienter slik at delforsøkene blir uavhengige.

Jeg bruker GeoGebras sannsynlighetskalkulator til å bestemme $P (X = 9)$ .

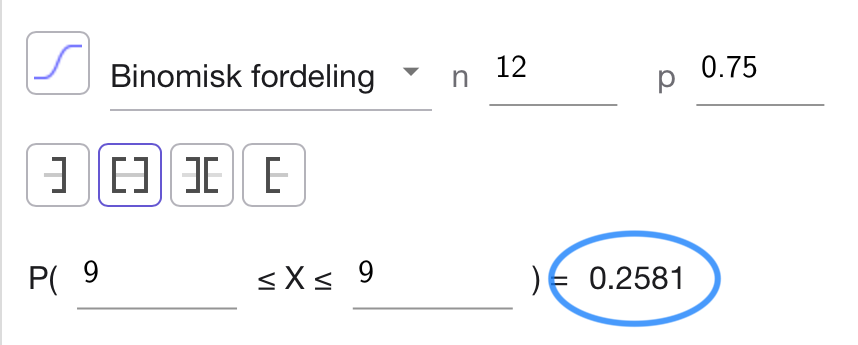
Utklipp til oppgave 2-2a

P (X = 9) = \underset{―}{\underset{―}{0,258}}

Utregning med formel for binomisk

Du kan også finne denne punktsannsynligheten enkelt med formelen for binomisk sannsynlighetsfordeling

P (X = k) = (\binom{n}{k}) \cdot p^{k} \cdot (1 - p)^{n - k}

P (X = 9) = (\binom{12}{9}) \cdot 0, 75^{9} \cdot 0, 25^{3} = 0,258 1

2-2b

Nullhypotesen vår er at begge legemidlene er like effektive, mens den alternative hypotesen er at legemiddel B er bedre.

\begin{array}{r} H_{0} : p = 0, 75 \\ H_{A} : p > 0, 75 \end{array}

Jeg finner sannsynligheten for at legemiddel B skal ha fungert på 9 av 10 pasienter gitt at $H_{0}$ er sann ved hjelp av GeoGebra.

Utklipp til oppgave 2-2b

$p$ -verdien er 0,244, dette er større enn signifikansnivået 0,05. Vi kan ikke forkaste $H_{0}$ , og vi kan dermed ikke si at legemiddel B fungerer bedre enn legemiddel A.

2–2c

Oppgaven kan også løses med binomisk fordeling

Denne oppgaven lar seg fint løse i GeoGebra ved å prøve seg fram med binomisk fordeling. Av gammel vane har jeg valgt å bruke normalfordeling som en tilnærming til den binomiske. Dette gir meg også mulighet til å skrive inn signifikansnivået 0,05 i svarfeltet i sannsynlighetskalkulatoren i GeoGebra.

Siden $Var (X)$ er høy så er normalfordelingen en veldig god tilnærming, og vi får samme svar uansett hvilken fordeling vi velger.

Jeg lar $Y$ være antallet pasienter som legemiddel B fungerer for av de 200 pasientene. $Y$ er tilnærmet normalfordelt siden $(Var (Y) = 200 \cdot 0, 75 \cdot 0, 25) ≫ 5$ .

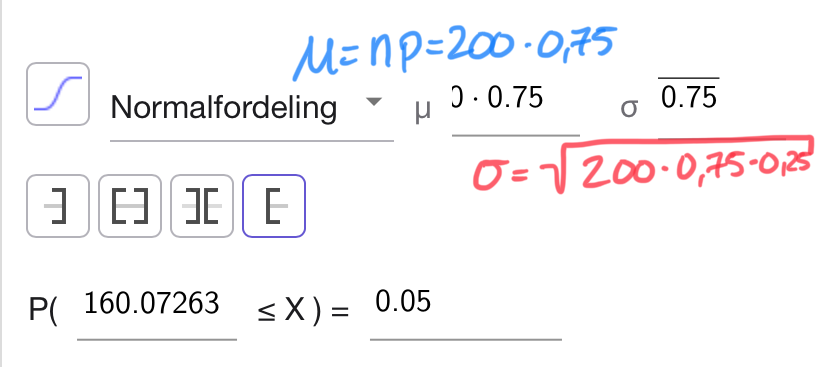
Utklipp til oppgave 2-2c

Jeg legger inn normalfordelingen med $μ = 200 \cdot 0, 75$ og $σ = \sqrt{200 \cdot 0, 75 \cdot 0, 25}$ . Deretter la jeg inn signifikansnivået 0,05 i svarfeltet, det gir oss at $Y$ må være minst 160,07. Vi må runde opp til 161 for å være sikre på at $p$ -verdien blir lavere enn signifikansnivået.

For å konkludere med at legemiddel B virker bedre enn A må det virke på minst 161 av de 200 pasientene.

Oppgave 2-3

Jeg velger å løse disse oppgavene i CAS, men jeg har tatt med et eksempel på løsning i regneark på oppgave 3c), se nedenfor.

Utklipp til oppgave 2-3

2-3a

Summen av nåverdiene til terminbeløpene skal bli lik lånebeløpet. Jeg setter opp dette som en likning i CAS med Sum((x/1.055^i), i, 1, 25) = 25000000 og løser, se linje 1 i utklippet.

Terminbeløpet er 186 373 kr.

2-3b

Jeg setter opp det det ekstra lånet som et nytt lån til samme rente med 20 års nedbetalingstid. Jeg regner ut terminbeløpet til dette lånet på samme måte som i a), og får terminbeløpet 41 839,67 kr. Se linje 2 i utklippet.

Olivia må betale for begge lånene fra år 5 og utover, se linje 3.

Det nye terminbeløpet blir 228 213 kr fra år 5 og utover.

2-3c

Etter 5 år så har Olivia allerede betalt ned lånet med kr 272 767, se linje 4.

I linje 5 så setter jeg opp en likning. På venstre side har vi summen av nåverdiene til terminbeløpene, men med ukjent antall terminer. På høyre side har vi lånebeløpet etter 5 år, som blir det originale lånebeløpet og ekstralånet, minus 272 767 kr. Fra CAS ser jeg at det tar 25,89 år etter de 5 første årene før lånet er nedbetalt. Jeg runder opp til 26 siden det er først i dette året at lånet er tilbakebetalt.

Den nye tilbakebetalingstiden blir 31 år.

Løsning med regneark

Det er mulig å gjøre alle deloppgavene i denne oppgaven i regneark (i hvert fall hvis du bruker målsøking).

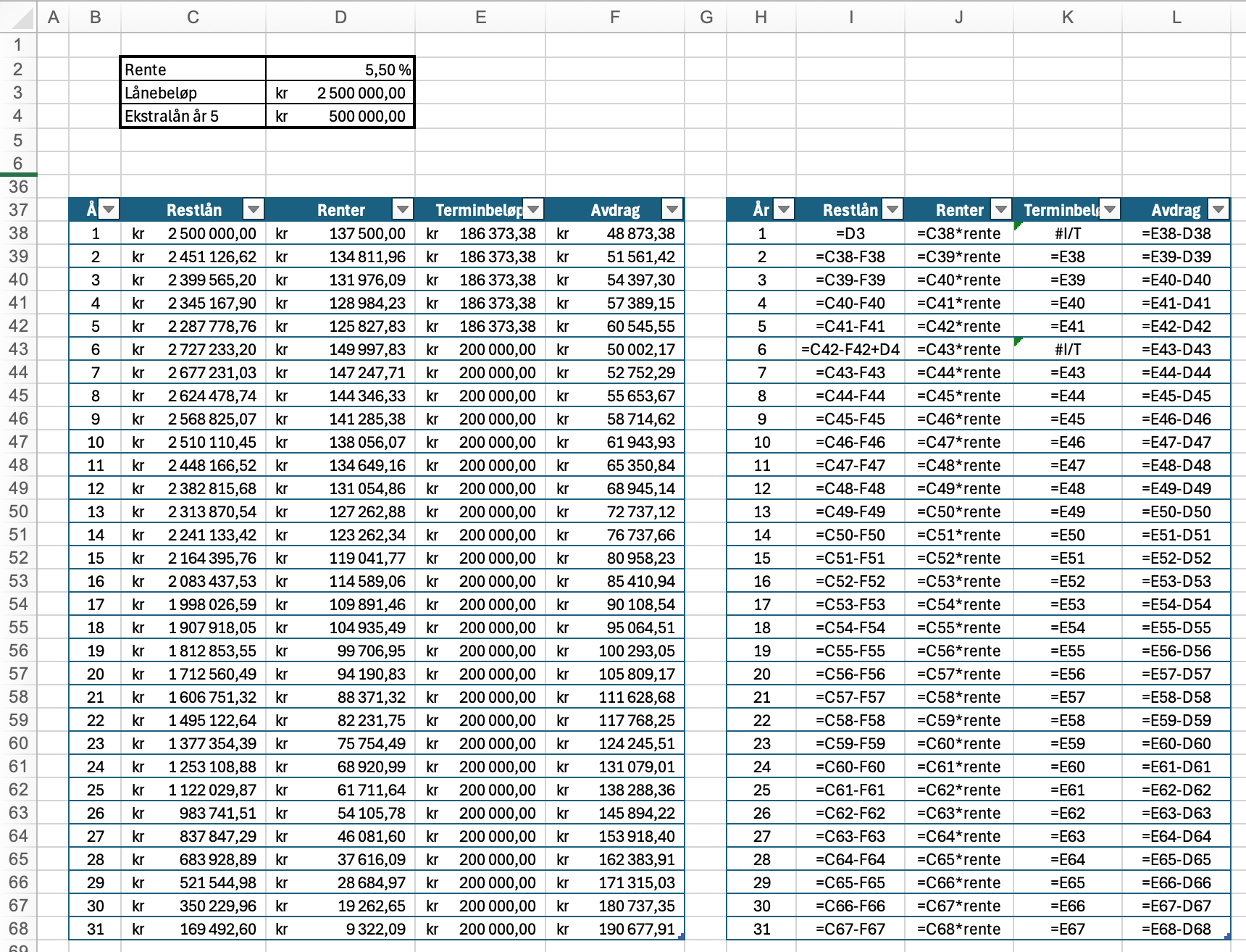
Nedenfor har jeg løst oppgave c) i regneark ved å sette opp lånet og beregne renter for hvert år. I år 5 så legger jeg til 500 000 kr ekstra på lånet (celle C43) og endrer terminbeløpet til 200 000 kr (celle E43).

Deretter fyller jeg bare formlene nedover og utvider tabellen fram til jeg ser at lånet er tilbakebetalt.

Som vi ser er lånet fullstendig tilbakebetalt i år 31 hvor avdragene er større enn restlånet.

Utklipp av regneark til oppgave 2-c

Oppgave 2-4

2-4a

Jeg setter opp de første leddene og ser om jeg finner en rekursiv sammenheng som jeg kan bruke.

\begin{aligned} S_{1} & = 1^{3} \\ S_{2} & = 1^{3} + 2^{3} = S_{1} + 2^{3} \\ S_{3} & = 1^{3} + 2^{3} + 3^{3} = S_{2} + 3^{3} \end{aligned}

Jeg ser at hvert ledd er det forrige leddet, pluss det neste kubikktallet. En rekursiv sammenheng mellom summene er altså

\underset{―}{\underset{―}{S_{n + 1} = S_{n} + (n + 1)^{3}}}

For å bestemme en eksplisitt formel brukte jeg regresjon i GeoGebra.

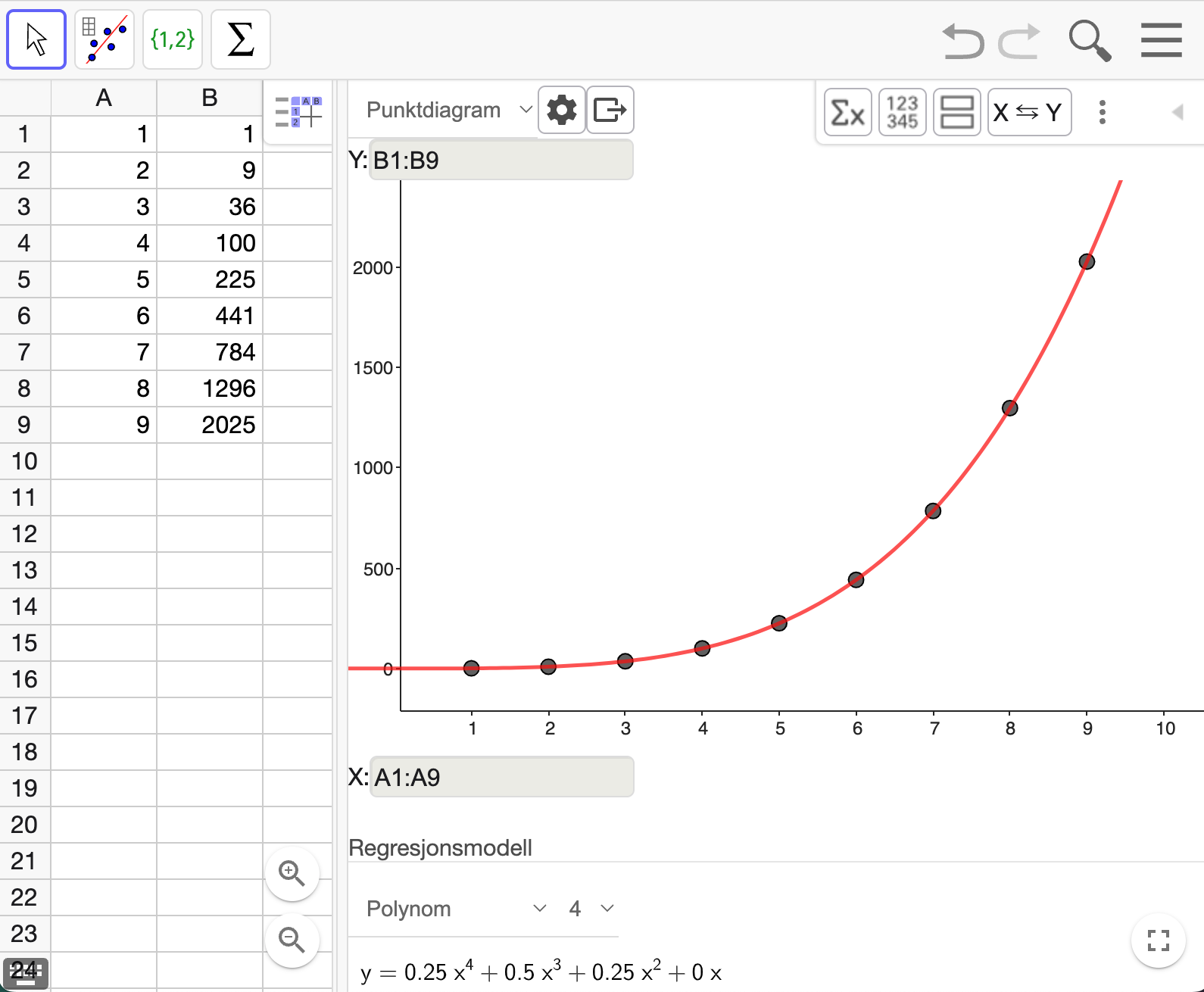
En eksplisitt formel for summene er

S_{n} = \underset{―}{\underset{―}{\frac{1}{4} (n^{4} + 2 n^{3} + n^{2})}}

2-4b

Jeg bruker følgende program

S = 0 # starter summen på 0

for n in range(1, 51):
	# kjører løkka 50 ganger
	S = S + n**3 #legger n^3 til S

print(S)

Programmet gir at $S_{50} = 1 625 625$ .

Oppgave 2-5

2-5a

Vi har et forsøk uten tilbakelegging med to typer baller, så vi kan bruke en hypergeometrisk sannsynlighetsfordeling. Hvis det er 15 baller av hver type er sannsynligheten for å trekke 9 røde og 6 blå baller gitt ved

P (R = 9) = \frac{(\binom{15}{9}) (\binom{15}{6})}{(\binom{30}{15})} = 0,161

Sannsynligheten for å trekke 9 røde og 6 blå baller er 16,1 %.

2-5b

Løsningsmetode 1: Programmering

Her prøver jeg meg fram med programmering og setter inn ulike verdier for antallet baller i kurva. Man kan programmere binomialkoeffisientfunksjonen selv, eller bruke en ferdig funksjon fra math-biblioteket.

import math #math.comb er binomialkoeff.funksjonen

rod = 9
bla = 6

for n in range(18, 201, 2): 
	# lager ei løkke som tester alle partall fra 18 til og med 200
	n1 = int(n/2) # halvparten av ballene er røde (må gjøre om til heltall)
	teller = math.comb(n1, rod) * math.comb(n1, bla)
	nevner = math.comb(n, (rod+bla))
	ssh = teller / nevner

	print(f"Ved {n} baller P(R=9) = {ssh:.5f}")

Utskriften forteller meg at det mest sannsynlige antallet baller i kurven er 34 eller 36.

Bruk 2n istedenfor n/2

I mitt løsningsforslag har jeg gått ut fra at krukka inneholder $n$ baller. Det er nok lurere å si at det er $n$ røde baller i krukka, og at krukka samlet sett inneholder $2 n$ baller. Da slipper du å gjøre om $\frac{n}{2}$ til heltall med int().

Løsningsmetode 2: Funksjon

Jeg lager en funksjon hvor antall baller i kurva er ukjent.

f (x) = \frac{(\binom{\frac{x}{2}}{9}) (\binom{\frac{x}{2}}{6})}{(\binom{x}{15})}

Denne funksjonen er egentlig bare gyldig for partallene fra 18 og oppover, men jeg velger å tegne den uten begrensning i GeoGebra for å kunne finne ekstremalpunkter enkelt.

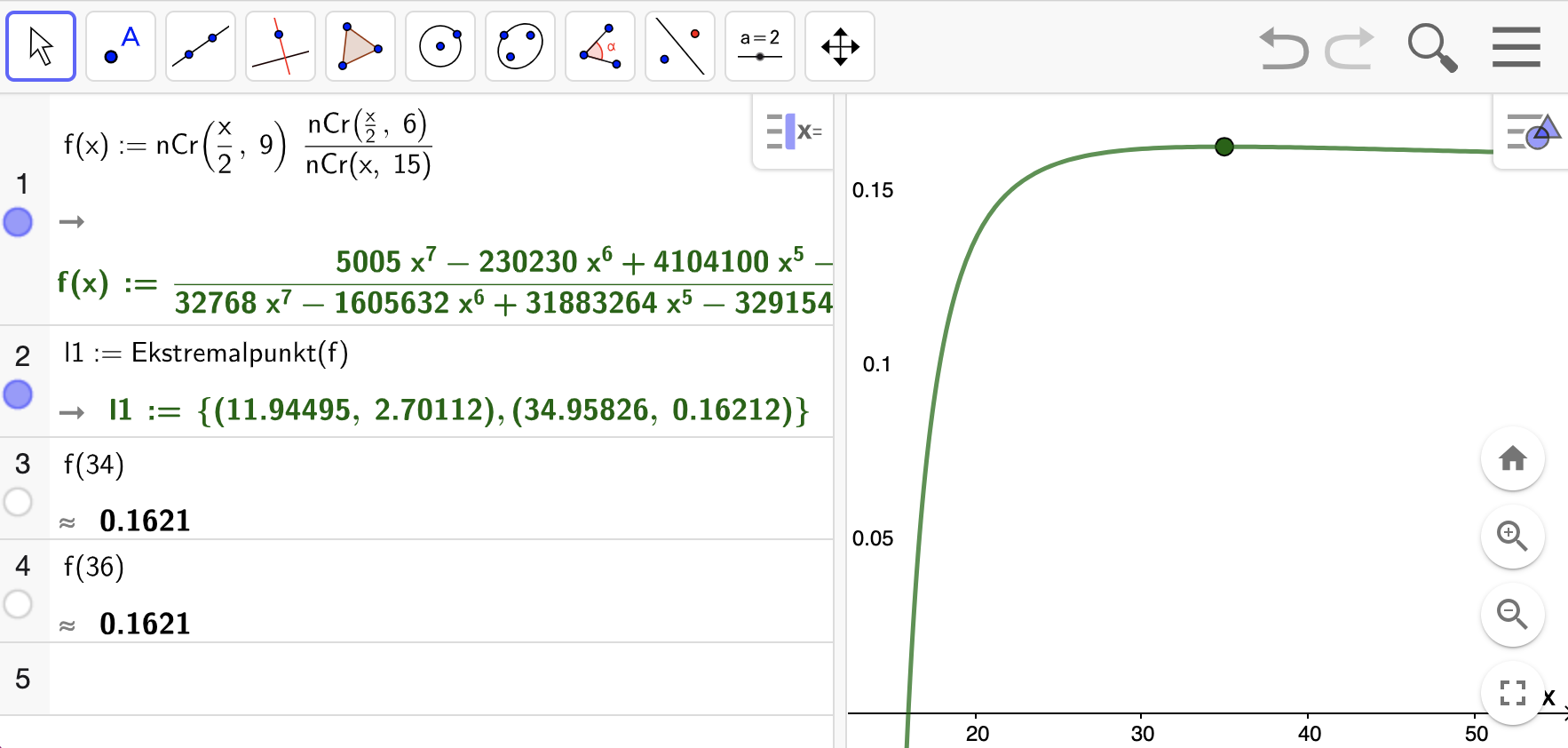
Jeg definerer funksjonen i CAS og finner ekstremalpunktet, se linje 1 og 2. Ekstremalpunktet ligger ved $x = 34, 96$ , dette er ikke en gyldig verdi for $x$ . Jeg tester derfor sannsynligheten ved $x = 34$ og $x = 36$ , begge disse er like store.

Det lå mest sannsynlig 34 eller 36 baller i kurven.