Løsningsforslag S2 eksamen V2025

Jeg blir veldig glad om du melder ifra om feil enten direkte til meg eller via forumet på matematikk.net.

Oppgave 1-1

1-1a

\int_{0}^{1} (2 e^{x} + 2 x^{2}) d x = {[2 e^{x} + \frac{2}{3} x^{3}]}_{0}^{1} = (2 e^{1} + \frac{2}{3} 1^{3}) - (2 e^{0} + \frac{2}{3} 0^{3}) = 2 e + \frac{2}{3} - 2 = \underset{―}{\underset{―}{2 e - \frac{4}{3}}}

1-1b

Vi ser at den deriverte av uttrykket i nevneren er det samme som telleren, og det er derfor lurt å forsøke variabelskiftet $u = x^{2} - x - 6$ .

u = x^{2} - x - 6 ⟹ \frac{d u}{d x} = 2 x - 1 ⟺ \frac{d u}{2 x - 1} = d x

Vi substituerer inn i det opprinnelige uttrykket

\int \frac{2 x - 1}{x^{2} - x - 6} d x = \int \frac{2 x - 1}{u} \frac{d u}{2 x - 1} = \int \frac{1}{u} d u = \ln | u | + C = \underset{―}{\underset{―}{\ln | x^{2} - x - 6 | + C}}

Løsning med delbrøkoppspalting

Hvis du velger å løse ved hjelp av delbrøkoppspalting så vil du etter faktorisering få følgende likning

2 x - 1 = A (x + 2) + B (x - 3)

Etter integrasjon får du svaret $\ln | x + 2 | + \ln | x - 3 | + C$ , som er det samme svaret som vi får med variabelskiftet skrevet på en annen form.

Oppgave 1-2

Vi vet at $f^{'} (x) = - \frac{2}{x^{3}}$ vil ha uendelig mange antideriverte med ulike konstantledd

\int - \frac{2}{x^{3}} d x = \int - 2 x^{- 3} d x = \frac{- 2}{- 2} x^{- 2} + C = \frac{1}{x^{2}} + C

Her er $C$ et hvilket som helst tall. Siden vi har fått vite at arealet av området som avgrenses av grafen til $f$ , $x = 1$ , $x = 2$ og $x$ -aksen er lik $\frac{11}{14}$ , samt at hele arealet ligger over $x$ -aksen, kan vi bruke et bestemt integral for å finne verdien av $C$ .

\begin{aligned} \int_{1}^{2} (\frac{1}{x^{2}} + C) d x & = \frac{11}{14} \\ \int_{1}^{2} (x^{- 2} + C) d x & = \frac{11}{14} \\ {[- \frac{1}{x} + C x]}_{1}^{2} & = \frac{11}{14} \\ (- \frac{1}{2} + C \cdot 2) - (- \frac{1}{1} + C \cdot 1) & = \frac{11}{14} \\ - \frac{1}{2} + 2 C + \frac{1}{1} - C & = \frac{11}{14} \\ C & = \frac{11}{14} - \frac{1}{2} = \frac{2}{7} \end{aligned}

Vår antideriverte til $f^{'} (x)$ har altså $C = \frac{2}{7}$ , derfor har vi for alle $x \neq 0$ :

\underset{―}{\underset{―}{f (x) = \frac{1}{x^{2}} + \frac{2}{7}}}

Oppgave 1-3

1-3a

$k$	1	2	3	6	Sum
$P (X = k)$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{1}{6}$	$\frac{3}{6} = \frac{1}{2}$	$1$
$k \cdot P (X = k)$	$\frac{1}{6}$	$\frac{2}{6}$	$\frac{3}{6}$	$\frac{18}{6}$	$\frac{24}{6} = 4$
$(k - μ)^{2} \cdot P (X = k)$	$3^{2} \cdot \frac{1}{6} = \frac{9}{6}$	$2^{2} \cdot \frac{1}{6} = \frac{4}{6}$	$1^{2} \cdot \frac{1}{6} = \frac{1}{6}$	$2^{2} \cdot \frac{3}{6} = \frac{12}{6}$	$\frac{26}{6} = \frac{13}{3}$

Vi finner forventningsverdien ved å finne summen av rad 3 siden $E (X) = \sum k \cdot P (X = k)$

Forventningsverdien $E (X) = \underset{―}{\underset{―}{4}}$

1-3b

Vi finner variansen ved å summere rad 4 i tabellen siden $Var (X) = \sum (k - μ)^{2} \cdot P (X = k)$

Variansen er $Var (X) = \underset{―}{\underset{―}{\frac{13}{3}}}$

Oppgave 1-4

1-4a

Her setter vi opp en oversikt for å se hvordan variablene i programmet utvikler seg.

`i`	`a`	Beregning av neste `a`
1	2	$2 + 1 + 2 = \underset{―}{5}$
2	5	$5 + 2 + 2 = \underset{―}{9}$
3	9	$9 + 3 + 2 = \underset{―}{14}$
4	14	$14 + 4 + 2 = \underset{―}{20}$
5	20

Vi ser en tallfølge hvor differansene mellom leddene starter på 3, og deretter øker med 1 for hvert ledd. Matematisk kan dette uttrykkes med den rekursive sammenhengen

a_{n + 1} = a_{n} + n + 2

Koden skriver ut leddene i tallfølgen $\underset{―}{\underset{―}{2, 5, 9, 14, 20}}$ .

1-4b

Eleven har lagt til en variabel S. S gir en løpende sum av verdiene til a, derfor vil S være delsummen til rekka etter n ledd.

Eleven ønsker å finne delsummen til rekka etter 5 ledd, altså $2 + 5 + 9 + 14 + 20 = \underset{―}{\underset{―}{50}}$

Oppgave 1-5

1-5a

Enhetskostnaden når det produseres 180 enheter er gitt ved

E (180) = \frac{K (180)}{180} = \frac{14 920}{180} = 82, 89

Du trenger ikke regne ut delestykket over

Du trenger ikke regne ut $\frac{14920}{180}$ siden du har fått oppgitt en linje fra origo til punktet $(180, 14 920)$ . Stigningstallet til en rett linje er jo $\frac{Δ y}{Δ x}$ , og i vårt tilfelle vil $K (180) = Δ y$ og $180 = Δ x$ . Denne linja har stigningstallet $82, 89$ , derfor må $\frac{Δ y}{Δ x} = \frac{14920}{180} = 82, 89$

Grensekostnaden er den deriverte av kostnadsfunksjonen, og grensekostnaden ved 180 enheter er derfor lik stigningstallet til tangenten til $K$ ved $x = 180$ . Jeg leser av stigningstallet til tangenten og finner at grensekostnaden er 138.

Enhetskostnaden ved 180 enheter er 82,89 kr/enhet og grensekostnaden er 138 kr/enhet.

1-5b

For at vi skal ha størst overskudd må $I^{'} (x) = K^{'} (x)$ . Vi bestemmer grenseinntekten.

I (x) = p \cdot x ⟹ I^{'} (x) = p

For å finne prisen som gir størst overskudd ved produksjon og salg av 180 enheter så setter vi opp $I^{'} (180) = K^{'} (180)$ .

I^{'} (180) = K^{'} (180) ⟺ p = 138

Prisen 138 kr gir oss størst overskudd ved produksjon og salg av 180 enheter.

Oppgave 1-6

1-6a

Vi ønsker å teste om den nye bensinen gir bedre drivstofføkonomi enn den gamle. La $μ$ være forventningsverdien for kjørelengde per L for den nye bensinen. Da er hypotesene våre:

\begin{array}{r} H_{0} : μ = 20 \\ H_{A} : μ > 20 \end{array}

1-6b

Denne hypotesetesten er av et gjennomsnitt. La $\bar{X}$ være gjennomsnittsverdien for drivstofføkonomien for et utvalg av biler. Etter sentralgrensesetningen er $\bar{X}$ normalfordelt med:

\begin{aligned} E (\bar{X}) & = μ = 20 \\ SD (\bar{X}) & = \frac{SD (X)}{\sqrt{n}} = \frac{2, 5}{\sqrt{25}} = \frac{2, 5}{5} = \frac{1}{2} \end{aligned}

Observasjonen vår er $\bar{X} = 21$ . Vi gjør om til standard normalfordeling:

z = \frac{\bar{X} - μ}{SD (\bar{X})} = \frac{21 - 20}{0, 5} = 2

Sannsynligheten for at $\bar{X}$ skal ligge mer enn 2 standardavvik over forventningsverdien er kan vi finne ved hjelp av den vedlagte normalfordelingstabellen.

P (Z > 2) = 1 - Φ (2) = 1 - 0,977 2 = 0,022 8

p-verdien er 0,0228, som er mindre enn signifikansnivået vårt. Vi kan dermed forkaste nullhypotesen om at den nye bensinen er like god som den gamle.

Oppgave 2-1

2-1a

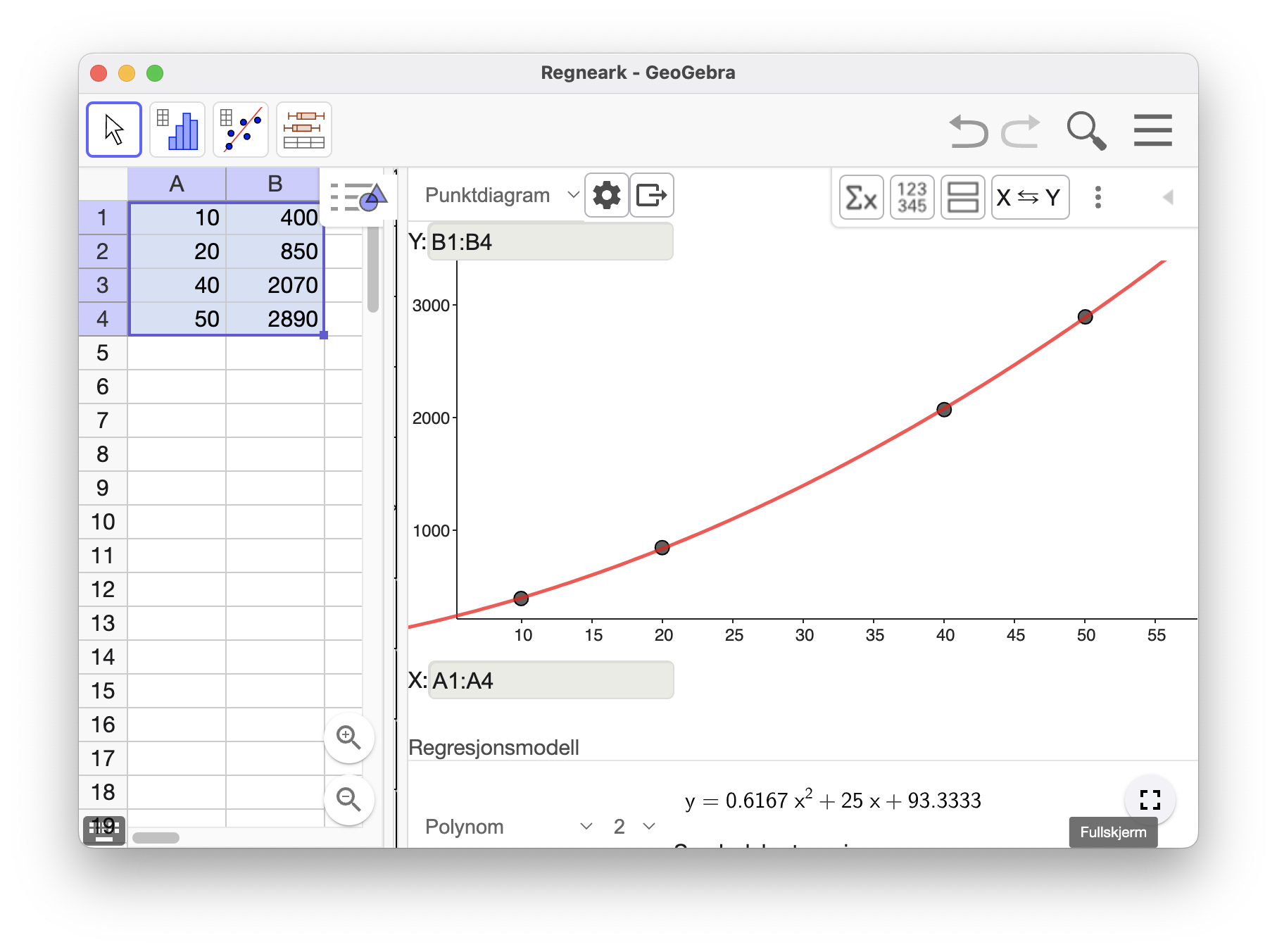
Regresjon i GeoGebra

Vi finner en andregradsmodell for kostnadene ved hjelp av regresjon i GeoGebra. Se utklippet over.

K (x) = 0,617 x^{2} + 25 x + 93, 33

Grenseinntekten $K^{'} (x) = 2 \cdot 0,617 x + 25 = \underset{―}{\underset{―}{1, 23 x + 25}}$ .

2-1b

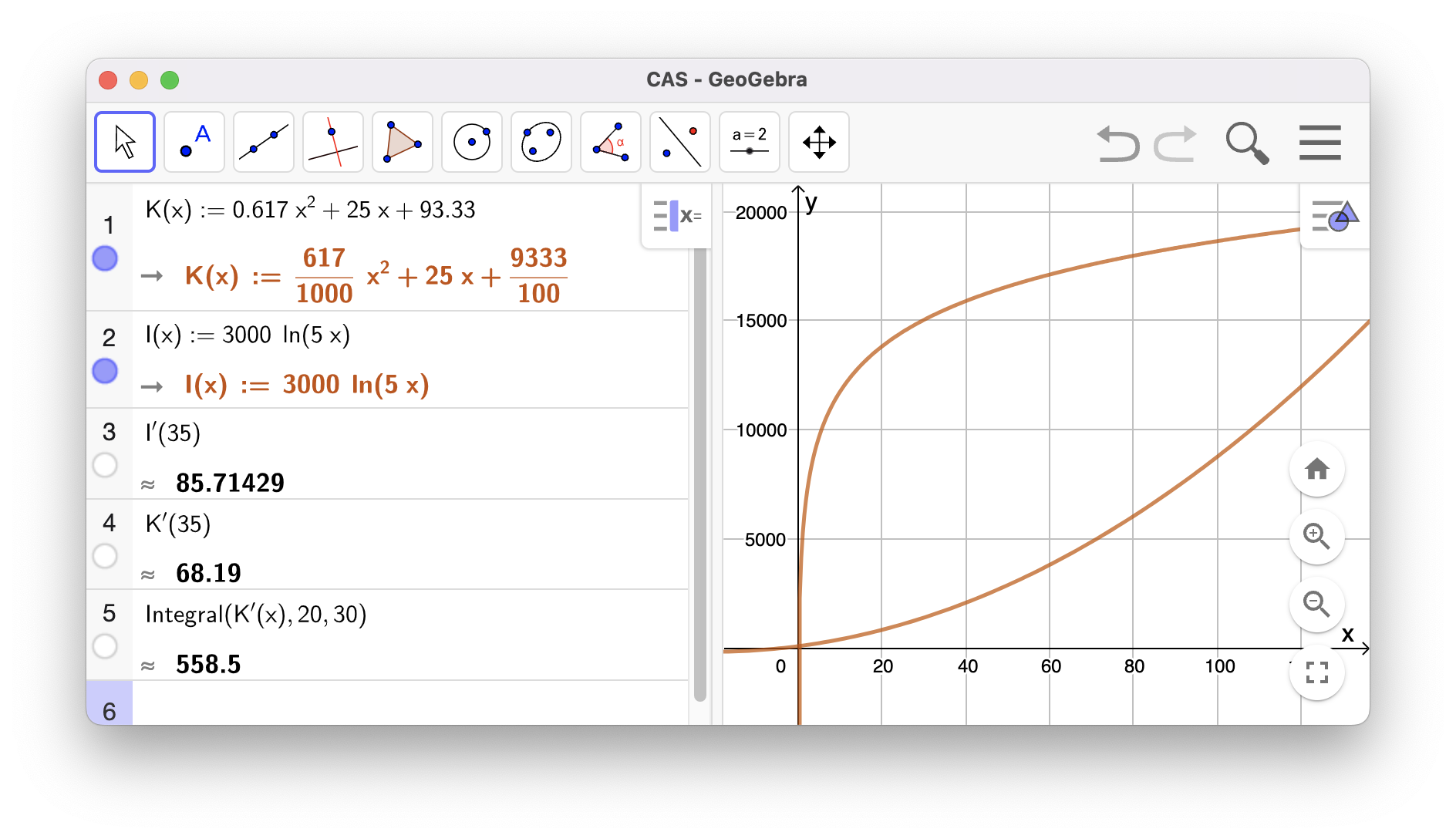
Grenseinntekt og grensekostnad i GeoGebra

Se linje 3 og 4 i CAS.

\underset{―}{\underset{―}{I^{'} (35) = 85, 71 og K^{'} (35) = 68, 19}}

Her øker grenseinntekten mer enn grensekostnaden, altså vil vi tjene mer penger (85,71 kr) på å produsere en mer enhet, enn hva vi må betale i produksjonskostnader for å produsere en mer enhet (68,19 kr). Vi tjener altså omtrent 17,5 kr på å produsere og selge 36 enheter framfor 35 enheter.

2-1c

Se linje 5 i CAS.

\underset{―}{\underset{―}{\int_{20}^{30} K^{'} (x) d x = 558, 5}}

Dette er det bestemte integralet av grensekostnaden $K^{'} (x)$ , altså vil svaret vårt tilsvare

\int_{20}^{30} K^{'} (x) d x = K (30) - K (20)

558,5 kr er altså differansen i produksjonskostnader mellom å produsere 20 enheter og 30 enheter.

Oppgave 2-2

La $B, M og E$ være lengdene av hoppene til henholdsvis Birger, Maren og Espen.

Vi bestemmer sannsynligheten for at hver av dem hopper 90 meter eller lengre ved hjelp av sannsynlighetsvinduet i GeoGebra, se skjermbildet under. (Kun Birgers utklipp er vist).

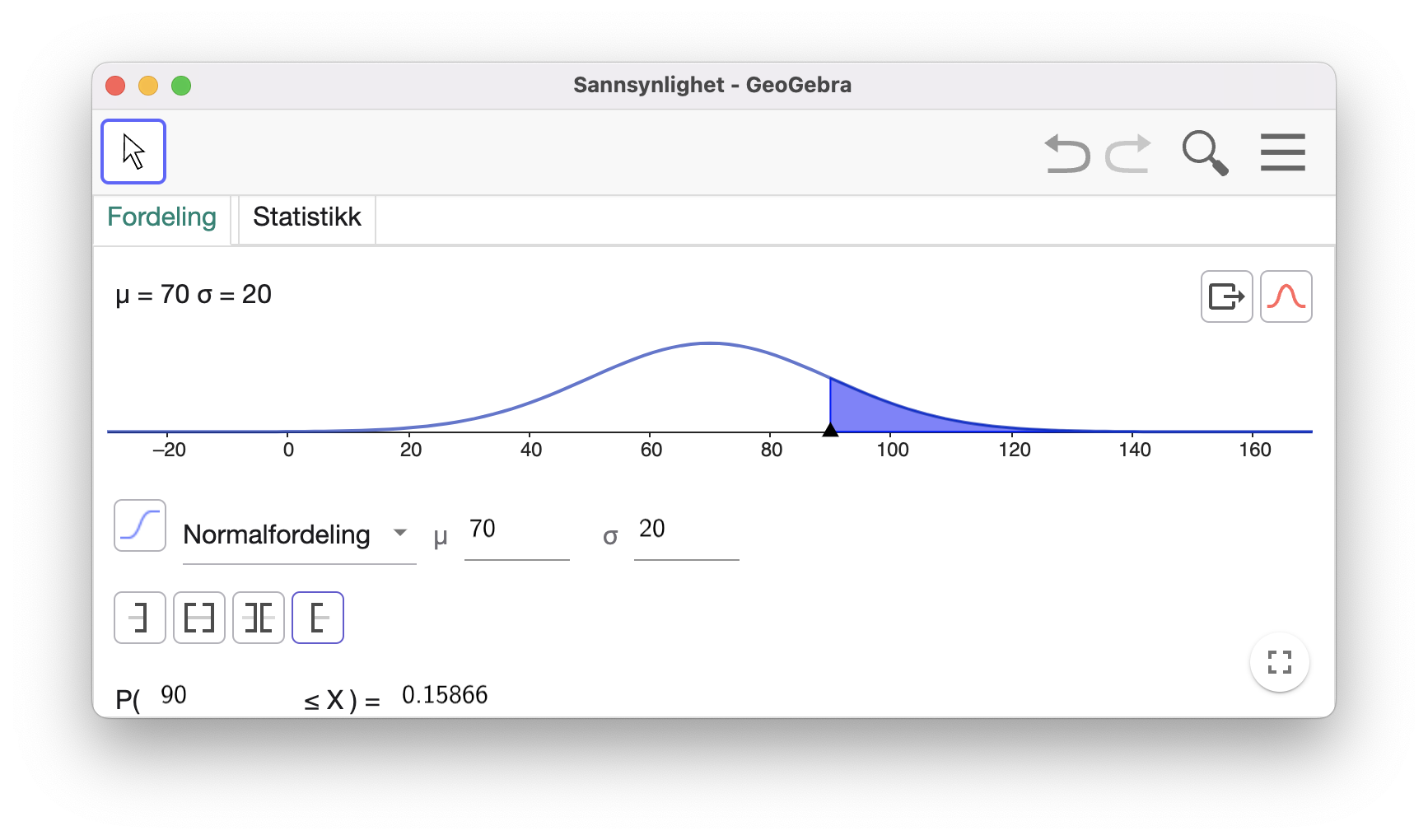
Sannsynligheten for at Birger hopper 90 meter eller lengre

P (B > 90) = 0,158 7, P (M > 90) = 0,022 8, P (E > 90) = 0,066 8

Sannsynlighetene for at Birger, Maren og Espen hopper lengre enn 90 meter er i ett tilfeldig hopp er henholdsvis 0,1587, 0,0228 og 0,0668.

2-2b

Hvis Maren skal hoppe lengst med et hopp på 83 meter så må både $B < 83$ og $E < 83$ . Vi kan bruke multiplikasjonsprinsippet for å finne sannsynligheten for at begge disse utfallene skjer samtidig. Igjen bestemmer vi sannsynligheten ved hjelp av sannsynlighetsvinduet i GeoGebra.

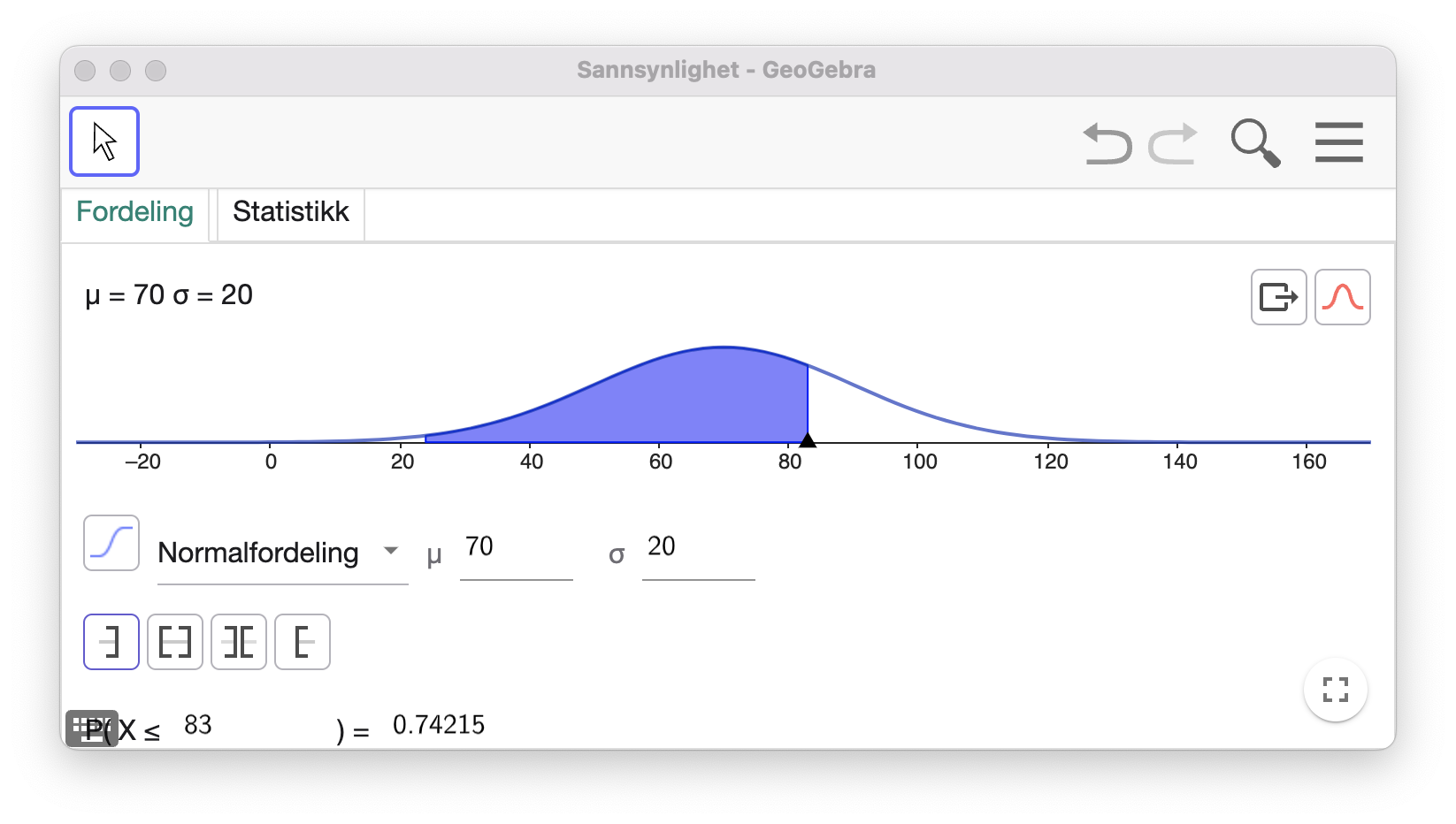
Sannsynligheten for at Birger hopper kortere enn 83 meter

\begin{aligned} P (Maren vinner med 83 m) & = P (B < 83) \cdot P (E < 83) \\ = 0,742 2 \cdot 0,788 1 = \underset{―}{\underset{―}{0,584 9}} \end{aligned}

Sannsynligheten for at Maren vinner med et hopp på 83 meter er 0,5849.

2-2c

Vi lager en simulering i Python hvor vi trekker hopplengder ut fra normalfordelingene til $B$ , $M$ og $E$ . Deretter sjekker vi om Marens hopp er det lengste hoppet.

from random import gauss
N = 100_000
antall_gunstige = 0

for i in range(N):
    # Trekker hopplengder fra normalfordelingene
    B = gauss(70, 20)
    M = gauss(80, 5)
    E = gauss(75, 10)

    # Sjekker om Marens hopp er lengre enn både Espens og Birgers
    if (M > B and M > E):
        antall_gunstige += 1

ssh = antall_gunstige / N

print(f"Det er omtrent {ssh * 100:.2f} % sannsynlighet for at Maren hopper lengst i andre omgang")

Etter å ha kjørt programmet flere ganger ser jeg at sannsynligheten er stabil på omtrent 47,4 %.

Det er omtrent 47,4 % sannsynlighet for at Maren hopper lengst i andre omgang.

Oppgave 2-3

Logistisk modell for brannalarmer i by

2-3a

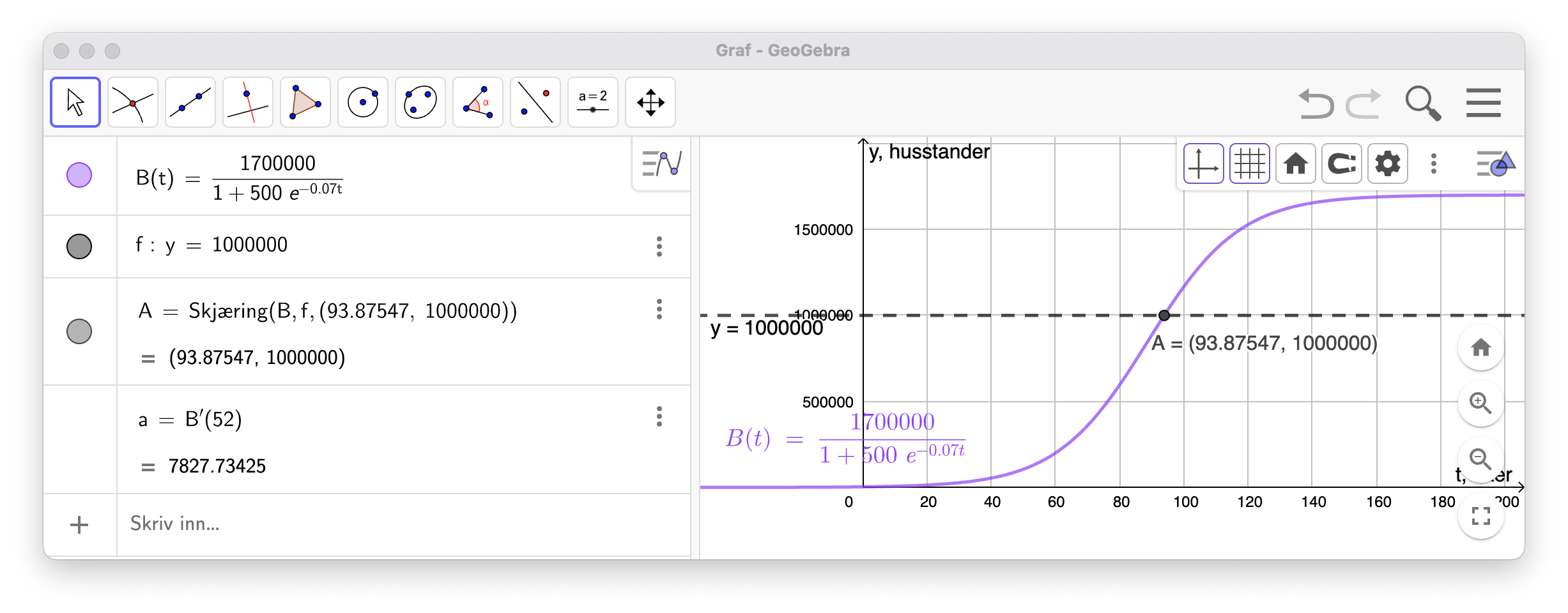
Jeg la inn modellen i GeoGebra og la inn linja $y = 1 000 000$ for å sjekke når halvparten hadde fått systemet. Jeg fant skjæringen med $B$ i punktet $A = (93, 88, 1000000)$ .

Det tar 94 uker før halvparten av husstandene i byen har brannvarslingssystemet ifølge modellen.

2-3b

Se nederst i GeoGebra-utklippet.

\underset{―}{\underset{―}{B^{'} (52) = 7827, 7}}

Etter 52 uker (ett år) så selges brannvarslingssystemet til omtrent 7828 husstander per uke.

2-3c

En logistisk modell er gitt ved

f (x) = \frac{N}{1 + a \cdot e^{- k x}}

$N$ er «bæreevnen» eller maksimalverdien for funksjonen
$\frac{N}{1 + a}$ vil være funksjonsverdien når $x = 0$
Vi har raskest vekst i vendepunktet som vi finner i $(\frac{\ln a}{k}, \frac{N}{2})$

Med bakgrunn i opplysningene i oppgaveteksten kan vi bestemme $N = 1 000 000$ siden dette er antallet husstander de totalt selger til.

Videre vet vi at det er 4000 husstander som har systemet ved $x = 0$ , derfor må

\frac{N}{1 + a} = 4000 ⟺ \frac{1000000}{1 + a} = 4000 ⟺ \frac{1000}{4} = 1 + a ⟺ a = 250 - 1 = 249

Til sist vet vi at vendepunktet (den raskeste veksten) er i uke 65, altså må

\frac{\ln a}{k} = 65 ⟺ \frac{\ln 249}{k} = 65 ⟺ 5,517 = 65 k ⟺ k = \frac{5,517}{65} = 0,084 9

En logistisk modell som passer til dataene vil være

\underset{―}{\underset{―}{F (t) = \frac{1 000 000}{1 + 249 e^{- 0,084 9 t}}}}

Løsning av 2-4 i CAS

Denne oppgaven kan også løses i CAS ved å sette opp 3 likninger for å bestemme $N$ , $a$ og $k$ , se skjermbildet under. Du kan også gjøre regresjon på punktene $(0, 4000)$ , $(65, 500 000)$ og $(200, 1 000 000)$ med logistisk modell.

Oppgave 2-4

CAS-løsning av 2-4

2-4a

Vi kaller det ukjente beløpet $B$ . Nora skal sette inn $B$ på konto 30 ganger. Det siste beløpet skal ha fått renter i 1 år, mens det første beløpet skal ha fått renter i 30 år.

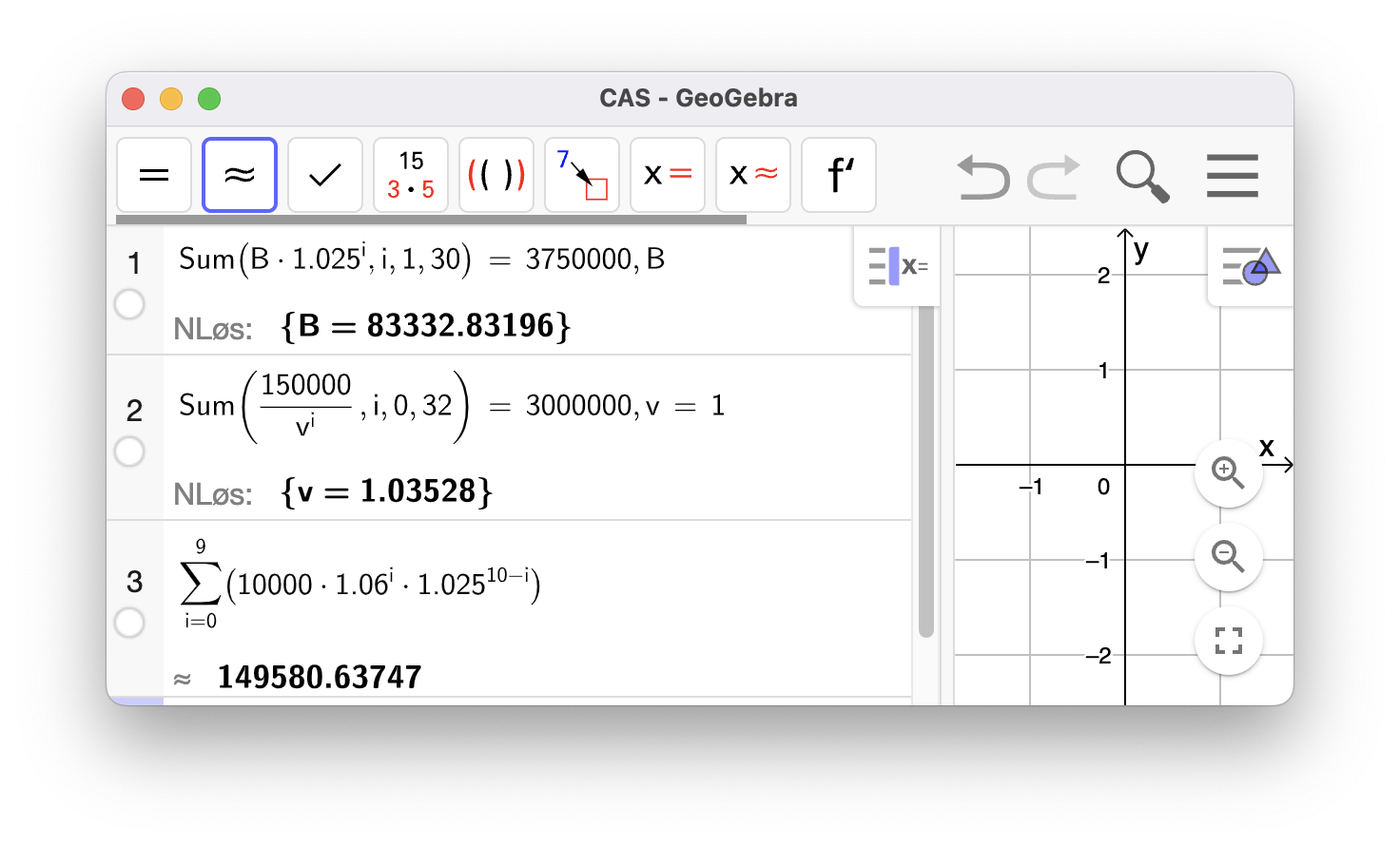
For å ha 3 750 000 kr på konto etter 30 år så kan vi altså sette opp en likning med ei rekke. Likningen er løst i linje 1 i GeoGebra.

\underset{År 2055}{\underset{⏟}{B \cdot {1,025}^{1}}} + \underset{År 2054}{\underset{⏟}{B \cdot {1,025}^{2}}} + \dots + \underset{År 2026}{\underset{⏟}{B \cdot {1,025}^{30}}} = 3 750 000

Nora må sette inn 83 333 kr hvert år for å nå målet.

2-4b

Vi kaller den ukjente vekstfaktoren til renta $v$ . Nora skal betale inn lånet over 33 terminer med første termin 1. januar 2026. Nåverdien (NV) til terminbeløpene vil være:

\underset{NV til 2026-beløpet}{\underset{⏟}{\frac{150 000}{v^{0}}}} + \underset{NV til 2057-beløpet}{\underset{⏟}{\frac{150 000}{v^{1}}}} + \dots + \underset{NV til 2058-beløpet}{\underset{⏟}{\frac{150 000}{v^{32}}}} = 3 000 000

Likningen er løst i linje 2 i GeoGebra.

Nora har regnet med at den årlige rentesatsen er 3,528 %.

2-4c

Sparebeløpene til Nora kan sees på som en rekke der det første beløpet er 10000 kr og får renter i 10 år, mens det siste beløpet er $10000 \cdot 1, 06^{9}$ og får renter i ett år.

\underset{Beløp år 0}{\underset{⏟}{10000 \cdot 1, 06^{0} \cdot {1,025}^{10}}} + \underset{Beløp år 1}{\underset{⏟}{10000 \cdot 1, 06^{1} \cdot {1,025}^{9}}} + \dots + \underset{Beløp år 9}{\underset{⏟}{10000 \cdot 1, 06^{9} \cdot {1,025}^{1}}}

Beløpet er beregnet i linje 3 i GeoGebra.

Nora vil ikke nå målet på 150 000 kr. Hun vil ha 149 581 kr på kontoen etter 10 år.

Alternativ løsning med målsøking i Excel

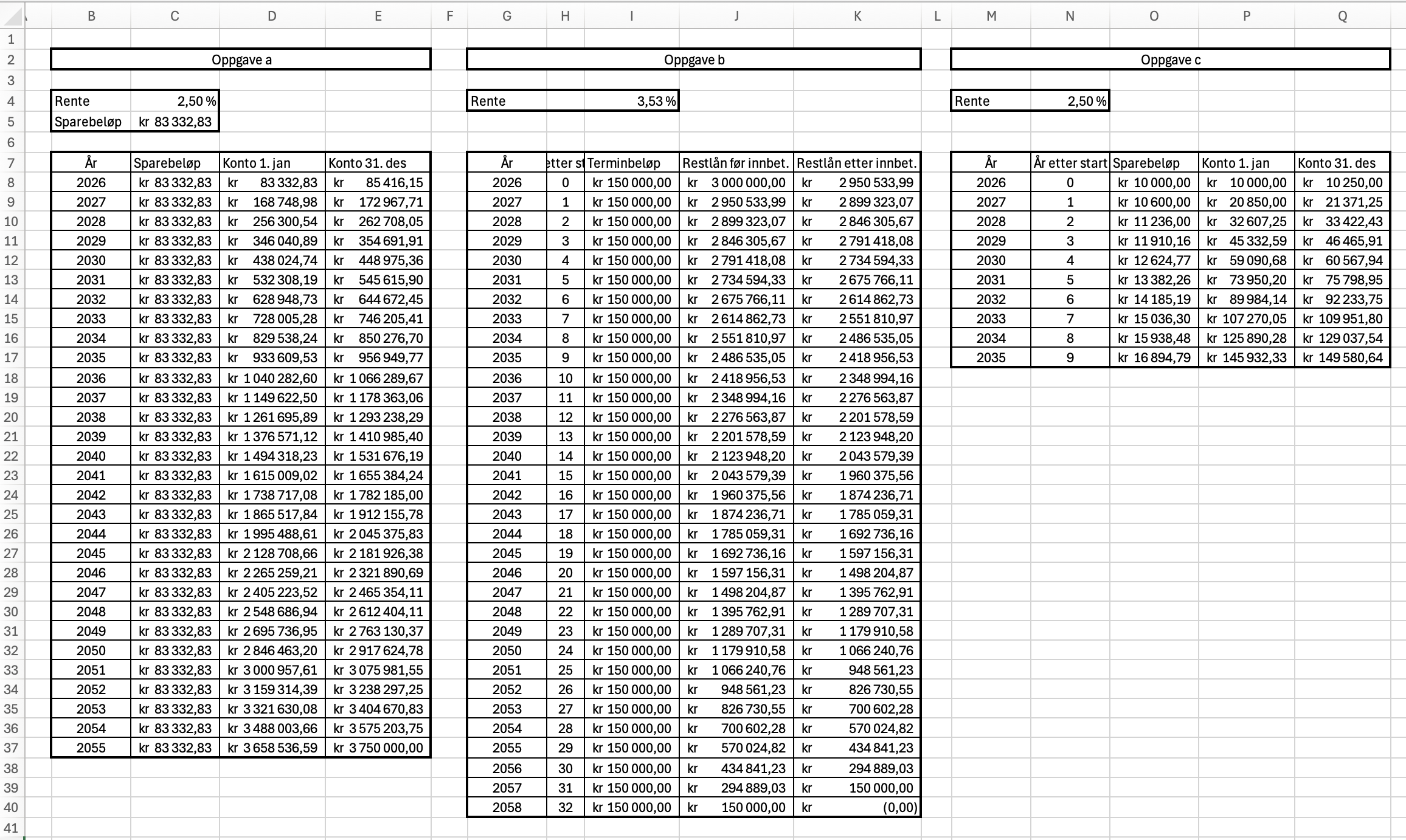
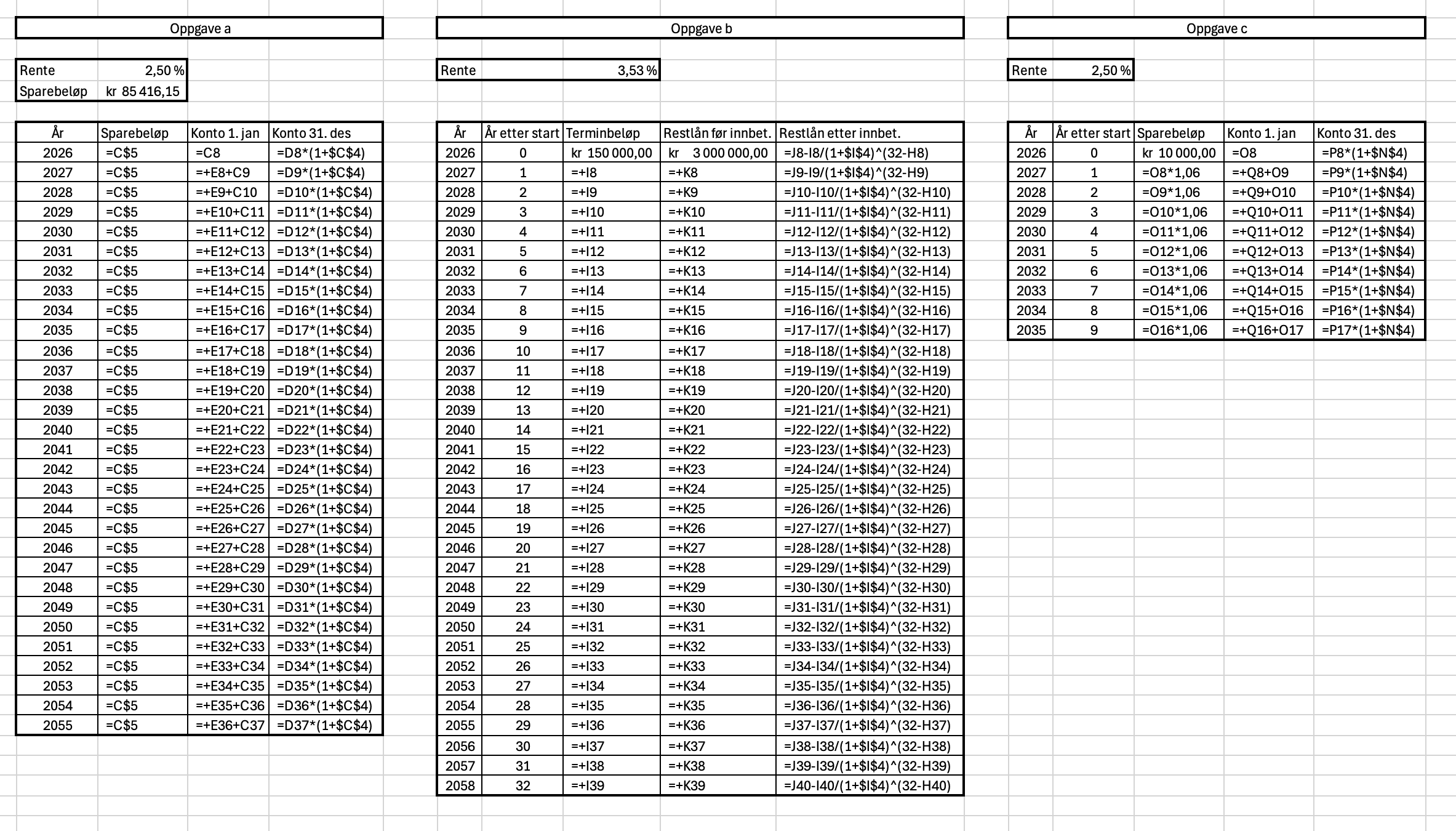
I regnearket nedenfor har jeg satt opp de tre deloppgavene i Excel for å løse med målsøking.

Oppgave a er løst ved å beregne innskuddet på kontoen i starten og slutten av hvert år. Noras sparebeløp er satt i celle C5. Ved å bruke målsøking og sette at celle C37 skal bli 3 750 000 kr ved å endre på C5 fikk jeg svaret 83 333 kr.

Oppgave b er løst ved å skrive inn restlånet 1. januar 2026, og beregne restlånene etter innbetaling hvert år. Restlånet etter innbetaling beregnes ved å sette avdraget lik $\frac{T}{v^{32 - i}}$ , der $v$ er vekstfaktoren til renta og $i$ er antall år siden 1. januar 2026. Renta ble funnet ved å gjøre målsøking der restlånet etter innbetaling skal være 0 kr i 2058.

Oppgave c. I denne oppgaven øker sparebeløpet med 6 % per år i kolonne O, samtidig som vi beregner renter i kolonner Q. I slutten av 2035 vil Nora ha 149 581 kr på konto.

Regneark for løsning av Noras sparing og lån

Formler for regneark med målsøking

Oppgave 2-5

Vi har fått oppgitt at

\begin{matrix} (1) & \int 1 d x + \int x d x + \int x^{2} d x + \int x^{3} d x + \dots = \int \frac{1}{1 - x} d x \end{matrix}

Vi gjennomfører resonnementet vårt i flere steg.

Integrasjon av høyre side

Vi ser først på høyre side av likning (1). Vi ser at vi kan integrere denne siden ved å gjøre variabelskiftet $u = 1 - x ⟹ \frac{d u}{d x} = - 1 ⟺ d x = - 1 \cdot d u$ .

Integralet blir (sett bort fra integrasjonskonstantene)

\int \frac{1}{1 - x} d x = \int \frac{1}{u} \cdot (- 1) d u = - \int \frac{1}{u} d u = - \ln | 1 - x |

Integrasjon av venstre side

Vi gjennomfører så integrasjonene på venstre av likning (1) i oppgaveteksten og får

\int 1 d x + \int x d x + \int x^{2} d x + \int x^{3} d x + \dots = x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + \frac{1}{4} x^{4} + \dots

Ved å integrere begge sidene av likning (1) har vi altså foreløpig vist at:

x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + \frac{1}{4} x^{4} + \dots = - \ln | 1 - x |

Vise at rekka er lik $\ln 2$

Vi skal vise at

\begin{matrix} (2) & \frac{1}{2^{1}} + \frac{1}{2} \cdot \frac{1}{2^{2}} + \frac{1}{3} \cdot \frac{1}{2^{3}} + \frac{1}{4} \cdot \frac{1}{2^{4}} + \dots = \ln 2 \end{matrix}

Vi sammenligner venstre side i likning (2) med svaret vi fikk da vi integrerte venstre side i likning (1).

\begin{matrix} (3) & x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + \frac{1}{4} x^{4} + \dots = \frac{1}{2^{1}} + \frac{1}{2} \cdot \frac{1}{2^{2}} + \frac{1}{3} \cdot \frac{1}{2^{3}} + \frac{1}{4} \cdot \frac{1}{2^{4}} + \dots \end{matrix}

Ved sammenligning av leddene ser vi at $x = \frac{1}{2}$ er en løsning av likning (3).

Siden $x = \frac{1}{2}$ , så sjekker vi hva $- \ln | 1 - x |$ gir oss når $x = \frac{1}{2}$

- \ln | 1 - x | = - \ln | 1 - \frac{1}{2} | = - \ln \underset{| \frac{1}{2} | = \frac{1}{2}}{\underset{⏟}{| \frac{1}{2} |}} = \underset{Regel: \ln (\frac{a}{b}) = \ln a - \ln b}{\underset{⏟}{- \ln (\frac{1}{2}) = - ({\ln 1}^{0} - \ln 2)}} = \ln 2

Vi har altså vist at

x + \frac{1}{2} x^{2} + \frac{1}{3} x^{3} + \frac{1}{4} x^{4} + \dots = - \ln | 1 - x |

Og for $x = \frac{1}{2}$ gjelder derfor:

\frac{1}{2^{1}} + \frac{1}{2} \cdot \frac{1}{2^{2}} + \frac{1}{3} \cdot \frac{1}{2^{3}} + \frac{1}{4} \cdot \frac{1}{2^{4}} + \dots = \ln 2