Skriv inn søketeksten i boksen over

Select a result to preview

Oppgaven er hentet fra eksamen 1T V23 del 2 oppgave 3.

Areal av firkant ved hjelp av trigonometri

Firkant

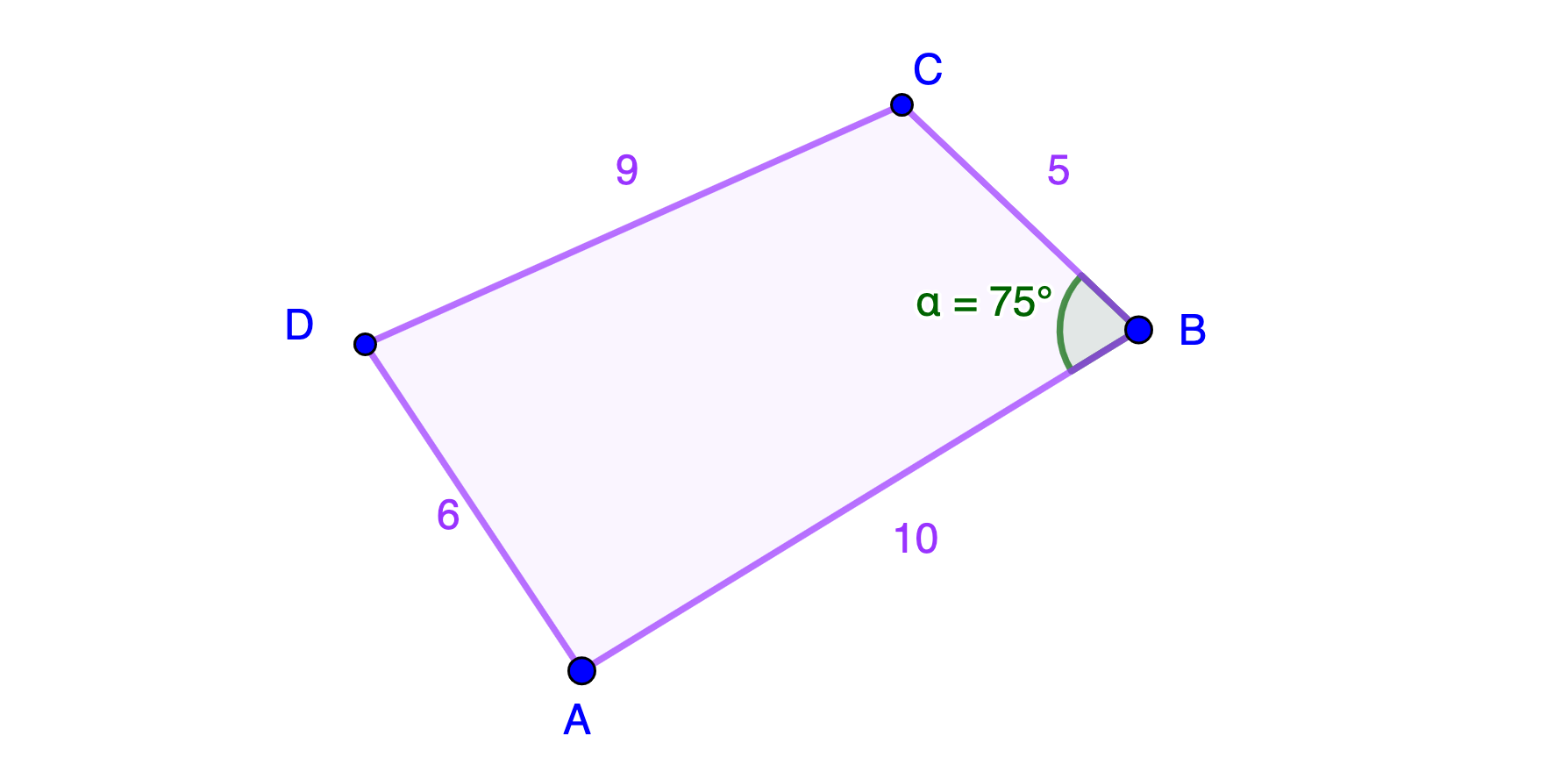
I denne oppgaven skal du vise at du kan bruke trigonometri til å bestemme arealet av figuren ovenfor.

Oppgave

Bestem arealet. Husk å gjøre rede for hvilke trigonometriske sammenhenger du bruker.

Kommentar

Kommentar: Du trenger ikke regne eksakte verdier i denne oppgaven, men du må bruke trigonometriske sammenhenger. Hvis du konstruerer firkanten i GeoGebra vil det ikke gi full uttelling.

Relatert

Tilfeldige oppgaver i samme fag

Det er ofte best å blande hvilke type oppgaver man gjør dersom du skal forberede deg til en prøve eller eksamen. Her er tre tilfeldige oppgaver i 1T.

Lignende oppgaver sortert etter tema

Trigonometri

Oppgave Fag År Oppg
Bevis for grenseverdien til sin v delt på v R2 V23 1-5
Omdreiingslegeme til trigonometrisk funksjon R2 V23 2-5
Tangens, derivert og integral R2 V23 1-2
Endevegg hus areal og takvinkel 1P-Y BA V23 2-1
Solcellepanel areal og kostnad 1P-Y EL V23 2-3
Trigonometri og effekttrekant 1P-Y EL V23 1-4
Areal av trekant i sirkel 1T V23 2-5
Begrunn hvorfor sin² u + cos² u = 1 1T V23 1-1
Vis at (sin u) / (cos u) = tan u 1T H22 1-1
Areal av område begrenset av sirkler GRUBLE Ingen Ingen
Areal av sirkel og kvadrat som skjærer hverandre 1T, R1, R2 Ingen Ingen
Areal av firekantet figur 1T H23 2-2
Areal mellom cosinus og sinus R2 H23 1-2
Likesidet trekant og cos 60° 1T H23 1-1
Luftforurensning og sinusfunksjon R2 H23 2-4
Strømproduksjon, trekant og resistans 1P-Y EL H23 1-4
Takstol til garasje 1P-Y BA H23 2-2
Tidevann og trigonometrisk modell R2 H23 2-1
To trekanter og størst areal 1T H23 1-4
Trekant med to løsninger 2P H23 2-5
Garasjeloft og trigonometri 1P-Y BA V24 1-5
Husvegg tak og solcellepaneler 1P-Y BA V24 2-2
Lysbrytning i vann 1T V24 2-2
Trekant med arealsetning og cosinussetning 1T V24 2-3
Trigonometri i rettvinklet trekant 1T V24 1-1
Sensor for utelys og trigonometri R2 V24 2-3
Sinusfunksjon og egenskaper R2 V24 1-5
Integral med delvis integrasjon og trigonometri R2 H24 1-1
Radianer og eksakte trigonometriske verdier R2 H24 1-4
Russebil med trigonometrisk fartsfunksjon R2 H24 2-4
Sinusfunksjon og cosinusfunksjon R2 H24 1-5
Trigonometrisk funksjon og likning R2 V25 1-4
Vinkel i sirkel og trigonometri R2 V25 1-7
Takstol og trekant ABC 1P-Y BA V25 2-1
Tolvkant innskrevet i sirkel 1T V25 2-3
Trigonometri med arealsetning og cosinus 1T V25 1-5
Sanne og usanne påstander om fart og vinkel R2 H25 1-5
Sinusmodell for elektrisk spenning R2 H25 2-2
Trigonometriske likninger og antall løsninger R2 H25 1-4
Vektorer, lengde og ortogonalitet R1 H25 2-5
App-ikon med sirkel og trekant 1P-Y IM H25 1-5
Areal av firkant med trigonometri 1T H25 2-3
Kledning og takkonstruksjon 1P-Y BA H25 2-1
Solcellepaneler og trigonometri 1P-Y EL H25 2-1
Trekantareal og sin 45 grader 1T H25 1-5
Bruke definisjonene av sinus og cosinus til å sette opp forhold 1P-Y EL H24 1-5
Lukas sin ukjente trekant 1P-Y EL V25 1-5
Bruk enhetssirkel til å finne sinus og cosinusverdier 1P-Y EL V24 1-4
Effekttrekant for motor Effekttrekant for motor 1P-Y EL H24 2-1
Felix sine effektdiagrammer Felix sine effektdiagrammer 1P-Y EL H25 1-5

Cosinussetningen

Oppgave Fag År Oppg
Areal av trekant i sirkel 1T V23 2-5
Areal av firekantet figur 1T H23 2-2
Trekant med arealsetning og cosinussetning 1T V24 2-3
Trigonometri med arealsetning og cosinus 1T V25 1-5

Arealsetningen

Oppgave Fag År Oppg
Areal av trekant i sirkel 1T V23 2-5
Areal av firekantet figur 1T H23 2-2
To trekanter og størst areal 1T H23 1-4
Trekant med arealsetning og cosinussetning 1T V24 2-3
Trigonometri med arealsetning og cosinus 1T V25 1-5
Trekantareal og sin 45 grader 1T H25 1-5

Geometri

Oppgave Fag År Oppg
Avstand fra punkt til linje og graf R1 V23 2-6
Likebeinte og formlike trekanter 2P V23 1-2
Parallellogram og vektorer R1 V23 2-2
Vinkler og vinkelrette vektorer R1 V23 1-3
Parallelle plan og kule R2 V23 2-2
Pyramide med fire punkter i rommet R2 V23 1-3
Sekskantmønster og vinkelsum 1P-Y IM V23 1-4
Solcellepanel areal og kostnad 1P-Y EL V23 2-3
Areal av område begrenset av sirkler GRUBLE Ingen Ingen
Areal av sirkel og kvadrat som skjærer hverandre 1T, R1, R2 Ingen Ingen
Kasse uten lokk S1, R1 H23 2-5
Areal av sideflaten i avkortet pyramide R2 H23 1-6
Ellipse og Ramanujans formel 1P H23 2-7
Plan, normalvektor og avstand til punkt R2 H23 1-4
Rektangel innskrevet i trekant 1P H23 2-5
Seilbåt med to seil og formlikhet 1P-Y NA H23 2-1
Takstol til garasje 1P-Y BA H23 2-2
Trekant med to løsninger 2P H23 2-5
Bindingsverk og kappliste for vegg 1P-Y BA V24 2-1
Blomsterkrukker og sylindervolum Sander 1P-Y NA V24 2-2
Formlike rammer og diagonal 1P-Y FD, 1P-Y DT V24 1-4
Garasjeloft og trigonometri 1P-Y BA V24 1-5
Husvegg tak og solcellepaneler 1P-Y BA V24 2-2
Logoer med parallellogrammer og symmetri 1P-Y IM V24 1-4
Sylinderformet lampe med hull 1P-Y FD, 1P-Y DT V24 2-1
Terrassestolper i betong sylinder 1P-Y TP V24 2-2
Kartmålestokk Oslo 2P V24 1-3
Klatrevegg rettavkortet kjegle 2P V24 2-5
Pyramide i halvkule – størst mulig volum S1, R1 V24 2-8
Tre punkter på linje og rettvinklet trekant R1 V24 1-4
Kuleflate og plan R2 V24 2-5
Trekant og plan i rommet R2 V24 1-4
Bindingsverk og kappliste for hytte 1P-Y BA H24 1-5
Blomsterpotte og likebeint trekant 1P-Y FD, 1P-Y TP, 1P-Y DT H24 1-5
Lykkehjul med sektorer og trekanter 1P-Y IM H24 1-4
Symmetri i logo 1P-Y IM H24 1-5
Vimpler i to størrelser 1P-Y FD, 1P-Y DT H24 1-4
Formlike trekanter og areal 2P H24 1-3
Volum og areal for lesehule 2P H24 2-8
Bordplate som trekant i 3D R2 V25 1-5
Areal og omkrets av halvsirkel og trekant 2P V25 1-4
Formlike trekanter over elv 2P V25 2-3
Vektorer og basketball R1 V25 1-6
Konusformet aksling og konisitet 1P-Y TP V25 1-5
Nomogram for omdreiningstall og boring 1P-Y TP V25 2-1
Parkbenk og svinn av terrassebord 1P-Y BA V25 1-4
Rom med skråtak og volum 1P-Y IM V25 1-4
Sylinderformede sittepuffer 1P-Y FD, 1P-Y DT V25 2-2
Takstol og trekant ABC 1P-Y BA V25 2-1
Tannhjul og skyvelære 1P-Y TP V25 1-4
Tolvkant innskrevet i sirkel 1T V25 2-3
Kuleflate og tangentplan R2 H25 1-7
Miniubåt, fart og kollisjon med fiskestim R2 H25 2-1
Volum av omdreiningslegeme – kopp R2 H25 1-2
Koordinater, linje og ortogonalitet R1 H25 1-4
Parameterframstilling og møtepunkt R1 H25 2-4
Grus på sti og kjeglehaug 2P H25 2-6
Modell av Eiffeltårnet 2P H25 1-3
Trekant i sirkel 2P H25 1-5
App-ikon med sirkel og trekant 1P-Y IM H25 1-5
Areal av firkant med trigonometri 1T H25 2-3
Blomsterbed med halvsirkel 1P H25 2-7
Breddegrader og jordomkrets 1P H25 2-6
Naomi sine søppelbøtter 1P-Y TP H25 2-2
Pyramide med proporsjonal høyde 1P H25 1-4
Rombe-duk og Pytagoras 1P-Y FD, 1P-Y DT H25 1-4
Solcellepaneler og trigonometri 1P-Y EL H25 2-1
Størst mulig rektangel under kurve 1T H25 2-5
Tangent til parabel og lagerhall 1T H25 2-6
Terrasse med Pytagoras 1P-Y BA H25 1-5