DEL 1 - Uten hjelpemidler

Oppgave 1-1

Vi skal finne hvor mange prosent prisen øker med når den går fra 300 kr til 315 kr.

Først finner vi økningen i kroner:

Økning = 315 - 300 = 15 kr

Deretter finner vi hvor mange prosent denne økningen utgjør av den opprinnelige prisen:

Prosentvis økning = \frac{Økning}{Opprinnelig pris} \cdot 100 % = \frac{15}{300} \cdot 100 % = \frac{1500}{300} % = 5 %

Prisen settes opp med $\underset{―}{\underset{―}{5 %}}$ .

Oppgave 1-2

Vi skal finne omtrent hvor mye studentene betaler til sammen for kollektivtransport i løpet av et år. Månedskortene koster omtrent 500 kr.

Vi regner ut totalbeløpet steg for steg:

\begin{aligned} Totalt beløp & = Antall studenter \cdot Pris per kort \cdot Antall kort per år \\ = 40 000 \cdot 500 \cdot 10 \\ = 40 000 \cdot 5000 \\ = 200 000 000 kr \end{aligned}

På standardform blir dette:

200 000 000 = 2 \cdot 10^{8}

Studentene betaler til sammen omtrent $\underset{―}{\underset{―}{2, 0 \cdot 10^{8} kr}}$ i løpet av et år.

Oppgave 1-3

Vi skal sortere tallene i stigende rekkefølge. Først skriver vi om tallene til desimaltall for å kunne sammenligne dem.

Vi regner ut verdien av hvert tall:

$4^{- 1} = \frac{1}{4^{1}} = 0, 25$
$3 \cdot 10^{- 1} = 3 \cdot 0, 1 = 0, 3$
$2^{0} = 1$
$\sqrt{2} = 1, 41 \dots$
$0, 02 \cdot 10^{2} = 0, 02 \cdot 100 = 2$
$\sqrt{80}$ er litt mindre enn $\sqrt{81} = 9$
$3^{2} = 9$

Stigende rekkefølge:

\underset{―}{\underset{―}{4^{- 1} < 3 \cdot 10^{- 1} < 2^{0} < \sqrt{2} < 0, 02 \cdot 10^{2} < \sqrt{80} < 3^{2}}}

Oppgave 1-4

1-4a

Vi vet at det er 20 vogner totalt. Fra tabellen kan vi finne hvor mange vogner som hadde personer i seg:

\begin{aligned} Vogner med personer & = 2 + 3 + 4 + 6 \\ = 15 vogner \end{aligned}

Antall tomme vogner blir da:

Tomme vogner = 20 - 15 = 5

Dette viser at Stines påstand er riktig - det var $\underset{―}{\underset{―}{5}}$ tomme vogner.

4b

Vi skal finne gjennomsnittet og medianen for antallet personer i hver vogn.

Gjennomsnitt:

For å finne gjennomsnittet må vi summere alle personene og dele på antall vogner:

\begin{aligned} Totalt antall personer & = 0 \cdot 5 + 1 \cdot 2 + 2 \cdot 3 + 3 \cdot 4 + 4 \cdot 6 \\ = 0 + 2 + 6 + 12 + 24 \\ = 44 personer \end{aligned}

Gjennomsnitt = \frac{44}{20} = 2, 2

Median:

For å finne medianen må vi sortere alle vognene etter antall personer. Vi har:

5 vogner med 0 personer
2 vogner med 1 person
3 vogner med 2 personer
4 vogner med 3 personer
6 vogner med 4 personer

Sortert liste: $0, 0, 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4$

Siden vi har 20 vogner (et partall), blir medianen gjennomsnittet av vogn nummer 10 og 11:

Median = \frac{2 + 3}{2} = 2, 5

Gjennomsnittet er $\underset{―}{\underset{―}{2, 2}}$ personer per vogn, og medianen er $\underset{―}{\underset{―}{2, 5}}$ personer per vogn.

4c

Kumulativ frekvens forteller oss hvor mange vogner som har to personer eller færre.

Framgangsmåte:

Vi summerer antall vogner med 0, 1 og 2 personer:

Kumulativ frekvens = 5 + 2 + 3 = 10

Praktisk tolkning: Den kumulative frekvensen for to personer er $\underset{―}{\underset{―}{10}}$ . Dette betyr at 10 vogner hadde 2 personer eller færre i seg. Med andre ord: halvparten av vognene var enten tomme eller hadde maksimalt 2 personer.

Oppgave 1-5

1-5a

To størrelser er proporsjonale hvis forholdet mellom dem er konstant. Dette gir en lineær sammenheng som går gjennom origo: $y = k \cdot x$ .

Analyse av grafene:

Grafen $q$ er en rett linje som går gjennom origo. Dette tyder på proporsjonale størrelser.

For å finne funksjonsuttrykket leser vi av et punkt på grafen. For eksempel ser det ut til at $q (4) = 600$ , som gir oss proporsjonalitetskontanten:

k = \frac{600}{4} = 150

Grafen $q$ beskriver sammenhengen mellom to proporsjonale størrelser, fordi den er en rett linje gjennom origo. Funksjonsuttrykket er $\underset{―}{\underset{―}{q (x) = 150 x}}$ .

1-5b

To størrelser er omvendt proporsjonale hvis produktet av dem er konstant: $y \cdot x = k$ , eller $y = \frac{k}{x}$ .

Analyse av grafene:

Grafen $r$ ser ut som en omvendt proporsjonal funksjon. Vi vet at to størrelser er omvendt proporsjonale dersom den ene størrelsen halveres når den andre dobles.

Vi leser av to punkter på grafen.

\begin{aligned} r (1) & = 1200 \\ r (2) & = 600 \end{aligned}

Vi ser altså at når $x$ dobles så halveres $y$ .

Grafen $r$ beskriver sammenhengen mellom to omvendt proporsjonale størrelser. Funksjonsuttrykket er $\underset{―}{\underset{―}{r (x) = \frac{1200}{x}}}$ .

Oppgave 1-6

1-6a

Vi skal finne antall pinner i figur 4 og figur 10.

Framgangsmåte:

La oss først se på mønsteret:

Figur 1: 3 pinner (én trekant)
Figur 2: 5 pinner (3 + 2)
Figur 3: 7 pinner (5 + 2)

Vi ser at hver ny figur får 2 flere pinner enn den forrige.

Figur 4:

Pinner i figur 4 = 7 + 2 = 9

Figur 10:

Vi kan fortsette mønsteret:

Figur 4: 9 pinner
Figur 5: 11 pinner
Figur 6: 13 pinner
Figur 7: 15 pinner
Figur 8: 17 pinner
Figur 9: 19 pinner
Figur 10: 21 pinner

Det vil være $\underset{―}{\underset{―}{9}}$ pinner i figur 4 og $\underset{―}{\underset{―}{21}}$ pinner i figur 10.

1-6b

Vi skal lage en formel for antallet pinner i figur $n$ .

Framgangsmåte:

Vi ser at:

Figur 1: $3 = 3 + 2 \cdot 0 = 3 + 2 (1 - 1)$
Figur 2: $5 = 3 + 2 \cdot 1 = 3 + 2 (2 - 1)$
Figur 3: $7 = 3 + 2 \cdot 2 = 3 + 2 (3 - 1)$
Figur $n$ : $3 + 2 (n - 1)$

Vi kan forenkle dette:

P (n) = 3 + 2 (n - 1) = 3 + 2 n - 2 = 2 n + 1

Formelen er $\underset{―}{\underset{―}{P (n) = 2 n + 1}}$ .

1-6c

Vi skal forklare hva programmet finner ut og hva verdiene som skrives ut betyr.

Analyse av programmet:

Programmet starter med:

n = 0 (figurnummer)
total = 0 (totalt antall pinner brukt)
figur = 3 (antall pinner i neste figur)
grense = 1000 (grensen for total)

I løkken:

n = n + 1: Går til neste figur
total = total + figur: Legger til pinnene fra denne figuren
figur = figur + 2: Neste figur får 2 flere pinner

Løkken fortsetter til total > 1000.

Resultat:

n = 31: Dette er figurnummeret
total = 1023: Dette er totalt antall pinner brukt

Programmet finner ut hvor mange figurer Vivian kan lage før hun har brukt over 1000 pinner totalt. Verdiene viser at etter å ha laget $\underset{―}{\underset{―}{31}}$ figurer har hun brukt $\underset{―}{\underset{―}{1023}}$ pinner totalt, som er første gang totalen overskrider 1000.

DEL 2 - Med hjelpemidler

Oppgave 2-1

2-1a

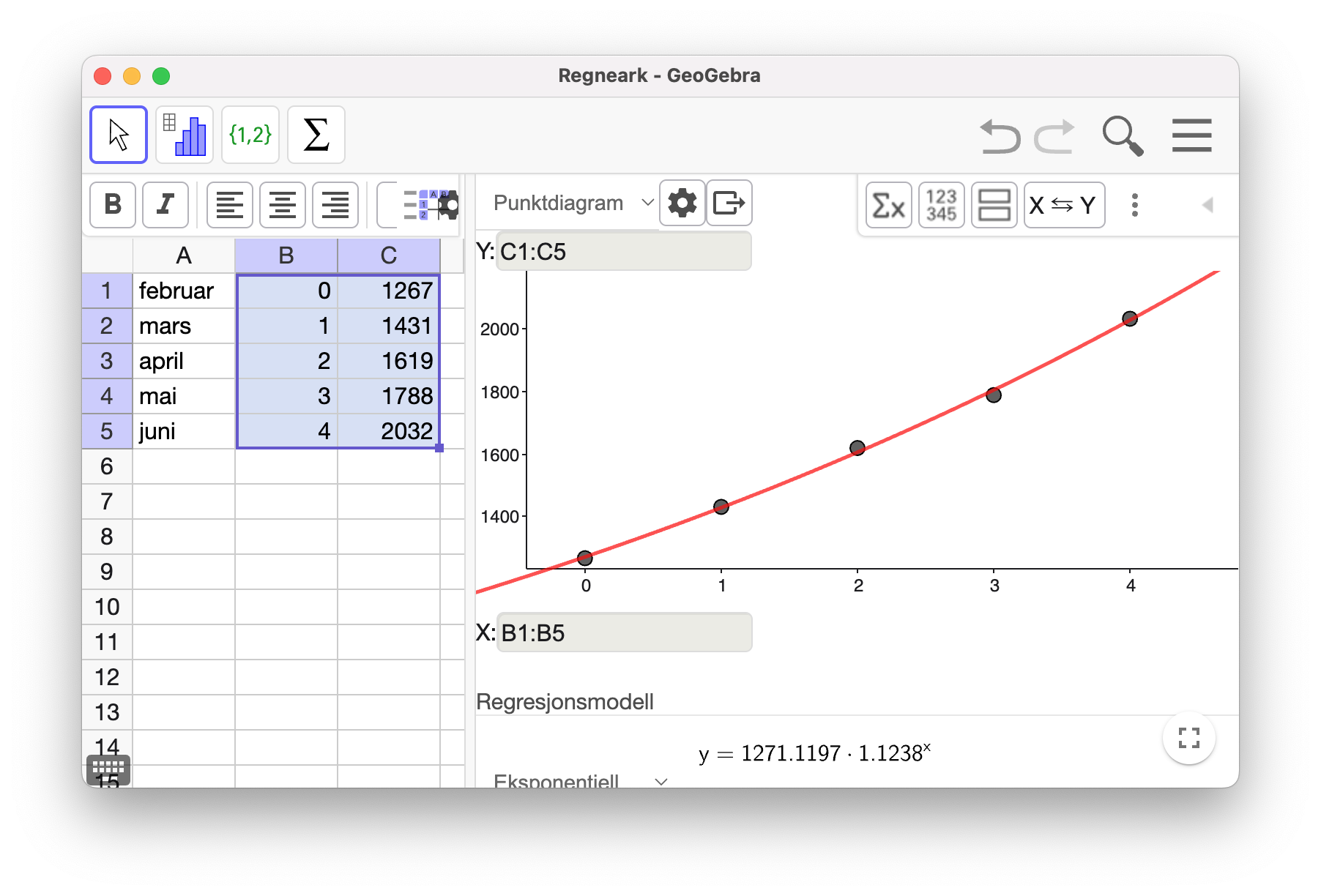
Regresjon for Alex sitt salg av hodepynt
Jeg la inn dataene i GeoGebra og brukte regresjon med en eksponentiell modell

Modellen $\underset{―}{\underset{―}{f (x) = 1271 \cdot {1,124}^{x}}}$ der $x$ er antall måneder etter februar 2025 passer godt for Alex' omsetning.

2-1b

Vekstfaktoren $b = 1,124$ tilsvarer $112, 4 %$ . Siden utgangspunktet vårt er 100 %, så blir økningen 12,4 %.

Omsetningen øker med omtrent $\underset{―}{\underset{―}{12, 4 %}}$ per måned ifølge modellen.

2-1c

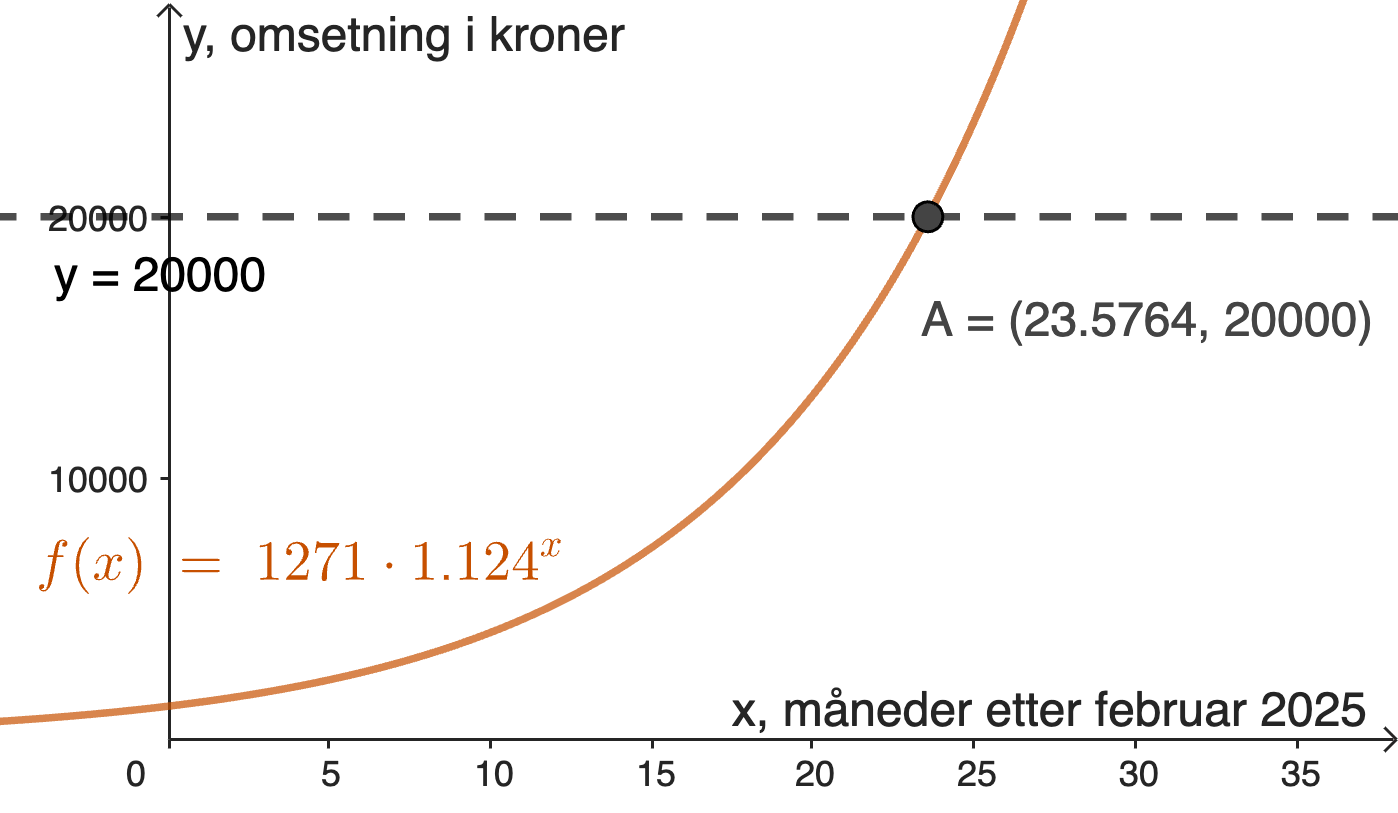
skjærer når omsetningen er 20 000 kr

Vi kan enten løse likningen $f (x) = 20000$ i CAS i GeoGebra, eller så kan vi finne skjæringen med linjen $y = 20000$ slik jeg har gjort i figuren-1c-graf, se punkt $A$ .

Alex kommer til å nå målet etter omtrent $\underset{―}{\underset{―}{23, 5}}$ måneder, det vil si i $\underset{―}{\underset{―}{januar 2027}}$ ifølge modellen.

2-1d

Vi skal finne hvor mange prosent omsetningen må øke med per måned etter juni 2025 for å nå målet i desember 2025.

Framgangsmåte:

I juni (måned 4) er omsetningen: $2032$ kr
Fra juni til desember er det 6 måneder
Vi vil nå 20 000 kr i desember

Vi kaller vekstfaktoren til økningen $x$ og setter opp likningen

2032 \cdot x^{6} = 20 000

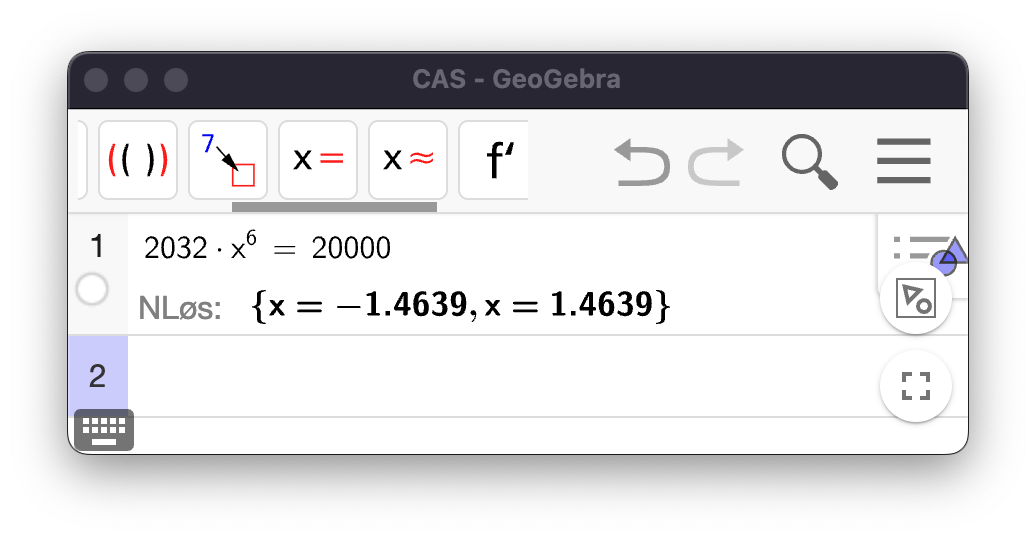
CAS-løsning av oppgave 2-1d

Denne vekstfaktoren tilsvarer 46,4 % økning.

Omsetningen må øke med omtrent $\underset{―}{\underset{―}{46, 4 %}}$ per måned etter juni 2025 for at Alex skal nå målet i løpet av desember 2025.

Oppgave 2-2

2-2a

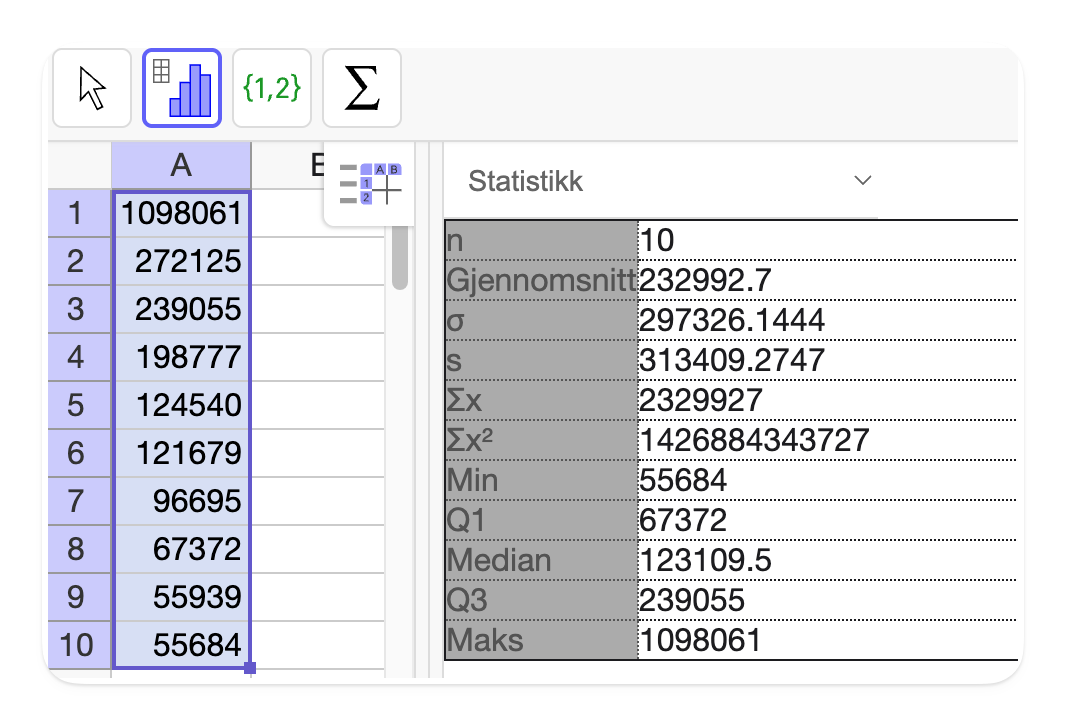
Beregning av sentralmål og spredningsmål i GeoGebra

Vi skal beregne median, gjennomsnitt, standardavvik og variasjonsbredde for innbyggertallet. Vi bruker regnearket i GeoGebra.

Variasjonsbredde:

Variasjonsbredde = Maks - Min = 1 098 061 - 55 684 = 1 042 377

Resultater:

Median: $\underset{―}{\underset{―}{123 110}}$
Gjennomsnitt: $\underset{―}{\underset{―}{232 993}}$
Standardavvik: $\underset{―}{\underset{―}{297 326}}$
Variasjonsbredde: $\underset{―}{\underset{―}{1 042 377}}$

2-2b

Vi ser at gjennomsnittet er nesten dobbelt så stort som medianen. Dette skyldes at Oslo (1 098 061) er en ekstremverdi som trekker gjennomsnittet kraftig opp.

Når vi har ekstremverdier i datasettet, er medianen et bedre sentralmål fordi den ikke påvirkes like mye av ekstreme verdier. Medianen viser den «midterste» verdien og gir et mer representativt bilde av et typisk stort tettsted i Norge.

Jeg er mest enig med Kine. Medianen er best å bruke fordi Oslo er en ekstremverdi som gjør gjennomsnittet misvisende. Medianen på 123 110 gir et mer representativt bilde av størrelsen på de norske tettstedene.

2-2c

Vi skal sammenligne folketallet i de danske og norske tettstedene.

Sammenligning:

Mål	Danmark	Norge
Gjennomsnitt	235 549	232 993
Median	67 832	123 110
Standardavvik	388 000	297 326

Observasjoner:

Gjennomsnittene er ganske like (Danmark litt høyere)
Medianen i Danmark er mye lavere enn i Norge (67 832 vs 123 110)
Standardavviket i Danmark er mye høyere (388 000 vs 297 326)

Tolkning:

Det høye standardavviket og den lave medianen i Danmark tyder på at København må være ekstremt mye større enn de andre danske tettstedene. I Norge er spredningen mindre - selv om Oslo er størst, er forskjellen til de andre byene ikke like dramatisk.

Danmark har en hovedstad (København) som dominerer mye mer enn Oslo gjør i Norge. De fleste danske tettstedene er relativt små (median 67 832), men København er så stor at den trekker gjennomsnittet opp og gir et svært høyt standardavvik. Norge har en jevnere fordeling av innbyggere mellom de største tettstedene.

Oppgave 2-3

Løsningen nedenfor er laget med KI

Jeg har ikke fått kontrollregnet denne løsningen enda.

Jeg skal lage en presentasjon med beregninger, diagrammer og kommentarer om nordmenns internettbruk.

Beregninger og funn:

Funn 1: Ungdom bruker mest tid på internett, og det øker mest for 16-24 år

La meg beregne gjennomsnittlig tid per aldersgruppe og økningen fra 2020 til 2024:

Aldersgruppe	2020	2024	Økning (min)	Økning (%)
9-15 år	180	245	65	36%
16-24 år	318	440	122	38%
25-44 år	245	338	93	38%
45-64 år	177	260	83	47%
65-79 år	60	127	67	112%

Kommentar: Aldersgruppen 16-24 år bruker mest tid på internett daglig (440 minutter = 7 timer og 20 minutter i 2024). Den største prosentvise økningen ser vi hos de eldste (65-79 år) som mer enn doblet sin internettbruk, men de bruker fortsatt minst tid totalt.

Funn 2: Alle aldersgrupper øker bruken, men mest markant etter 2021

La meg se på den årlige utviklingen:

Gjennomsnittlig tid på nett per dag for alle aldersgrupper:

2020: 196 minutter (3 timer 16 min)
2021: 213 minutter (3 timer 33 min)
2022: 259 minutter (4 timer 19 min) - STORT HOPP
2023: 260 minutter (4 timer 20 min)
2024: 282 minutter (4 timer 42 min)

Kommentar: Det er et markant hopp i internettbruken fra 2021 til 2022 (46 minutters økning). Dette kan muligens henge sammen med endrede vaner etter pandemien. Fra 2022 fortsetter bruken å øke, men i et roligere tempo.

Oppsummering av to interessante funn:

Unge voksne (16-24 år) er mest aktive på nett: De bruker i snitt over 7 timer daglig på internett i 2024, nesten dobbelt så mye som aldersgruppen 45-64 år. Den absolutte økningen (122 minutter) er også størst for denne gruppen.
Eldre gjør et digitaliseringshopp: Selv om 65-79-åringer fortsatt bruker minst tid på nett totalt, har de hatt den største prosentvise veksten (112% fra 2020 til 2024). Dette viser at også eldre blir stadig mer digitale, selv om de startet på et lavere nivå.

Oppgave 2-4

Løsningen nedenfor er laget med KI

Jeg har ikke kontrollert eller forbedredet denne løsningen enda.

Vi skal beregne hvor mye penger Fatima, Adrian og Vegard har ved starten av 2025.

Beregninger:

Fatima - Aksjefond med 36% vekst over 5 år

\begin{aligned} Verdi i 2025 & = 100 000 \cdot 1, 36 \\ = 136 000 kr \end{aligned}

Adrian - Sparekonto med 5,7% årlig rente

\begin{aligned} Verdi i 2025 & = 100 000 \cdot {1,057}^{5} \\ = 100 000 \cdot 1,319 4 \\ = 131 940 kr \end{aligned}

Vegard - Ulike aksjer med årlige endringer

Vi må regne år for år:

År	Vekstfaktor	Beregning	Verdi (kr)
Start (2020)	-	100 000	100 000
Etter 2020	1,20	$100 000 \cdot 1, 20$	120 000
Etter 2021	0,89	$120 000 \cdot 0, 89$	106 800
Etter 2022	0,90	$106 800 \cdot 0, 90$	96 120
Etter 2023	1,23	$96 120 \cdot 1, 23$	118 228
Etter 2024	1,17	$118 228 \cdot 1, 17$	138 326

Alternativ utregning i ett steg:

100 000 \cdot 1, 20 \cdot 0, 89 \cdot 0, 90 \cdot 1, 23 \cdot 1, 17 = 138 326 kr

Oversikt ved starten av 2025:

Person	Plassering	Verdi (kr)
Vegard	Ulike aksjer	138 326
Fatima	Aksjefond	136 000
Adrian	Sparekonto	131 940

Vegard har mest penger til tross for at han hadde to år med tap (2021 og 2022). De gode årene (2020, 2023 og 2024) veide opp for tapene. Adrian tjente minst fordi sparekontoen ga lavest avkastning over tid.

Oppgave 2-5

2-5a

Vi må anta jevn fordeling av aldre innenfor hvert intervall. Dermed blir midtpunktet en god tilnærmingsverdi for av gjennomsnittsalderen i gruppen.

2-5b

Vi bruker midtpunktet i hvert intervall:

Aldersintervall	Midtpunkt	Antall personer	Bidrag til sum
$[0, 18 ⟩$	9	188	$9 \cdot 188 = 1692$
$[18, 50 ⟩$	34	347	$34 \cdot 347 = 11 798$
$[50, 67 ⟩$	58,5	237	$58, 5 \cdot 237 = 13 865$
$[67, 80 ⟩$	73,5	103	$73, 5 \cdot 103 = 7571$
$[80, 90 ⟩$	85	33	$85 \cdot 33 = 2805$
$[90, 100 ⟩$	95	15	$95 \cdot 15 = 1425$

\begin{aligned} Sum alder & = 1692 + 11 798 + 13 865 + 7571 + 2805 + 1425 = 39 156 \\ Antall personer & = 188 + 347 + 237 + 103 + 33 + 15 = 923 \\ Gjennomsnittsalder & = \frac{39 156}{923} = 42, 4 år \end{aligned}

Gjennomsnittsalderen i Åseral kommune var $\underset{―}{\underset{―}{42, 4}}$ år i 2024.

2-5c

Gjennomsnittsalderen er 42,4 år. Vi må finne hvor mange som var eldre enn dette.

Intervallene som er helt over 42,4 år:

$[50, 67 ⟩$ : 237 personer
$[67, 80 ⟩$ : 103 personer
$[80, 90 ⟩$ : 33 personer
$[90, 100 ⟩$ : 15 personer

Sum: $237 + 103 + 33 + 15 = 388$ personer

Men vi må også inkludere noen fra intervallet $[18, 50 ⟩$ siden gjennomsnittsalderen (42,4 år) ligger i dette intervallet.

Hvis vi antar jevn fordeling i intervallet $[18, 50 ⟩$ :

Intervallet går fra 18 til 50 år (32 år bredt)
Vi vil ha de fra 42,4 til 50 år (7,6 år)
Andelen: $\frac{7, 6}{32} \approx 0,238$
Antall personer: $347 \cdot 0,238 \approx 83$ personer

Totalt antall over gjennomsnittet: $388 + 83 = 471$

Prosentandel:

\frac{471}{923} \cdot 100 % \approx 51, 0 %

Omtrent $\underset{―}{\underset{―}{51 %}}$ av befolkningen i Åseral kommune var eldre enn gjennomsnittsalderen i 2024.

Oppgave 2-6

Løsningen nedenfor er laget med KI

Jeg har ikke kontrollert eller forbedredet denne løsningen enda.

Svar til Nils

Nils' spørsmål: Er antallet julekuler og totalprisen proporsjonale størrelser?

Svar: Nei, de er ikke proporsjonale.

Forklaring:

To størrelser er proporsjonale hvis forholdet mellom dem alltid er det samme, altså $\frac{y}{x} = k$ (konstant). Dette gir en rett linje gjennom origo.

I dette tilfellet må klassen kjøpe både juletre OG julekuler. La oss si at:

Juletreet koster 500 kr (fast pris)
Hver julekule koster 20 kr

Da blir totalprisen:

Totalpris = 500 + 20 \cdot antall kuler

Dette er ikke en proporsjonal sammenheng fordi:

Hvis de ikke kjøper noen kuler: Pris = 500 kr (ikke 0 kr!)
Hvis de kjøper 10 kuler: Pris = 500 + 200 = 700 kr
Hvis de kjøper 20 kuler: Pris = 500 + 400 = 900 kr

Forholdet $\frac{pris}{antall kuler}$ endres hele tiden, så det er ikke proporsjonalt.

MEN: Hvis vi ser bort fra prisen på juletreet og bare ser på kuleprisene alene, da ville antall kuler og kuleprisene vært proporsjonale størrelser.

Svar til Hanne

Hannes spørsmål: Er beløpet hver må betale omvendt proporsjonalt med antall personer som deler?

Svar: Ja, det stemmer!

Forklaring:

To størrelser er omvendt proporsjonale hvis produktet av dem alltid er det samme, altså $x \cdot y = k$ (konstant), eller $y = \frac{k}{x}$ .

La oss si at det totale beløpet (juletre + kuler) er 800 kr. Da blir beløpet per person:

Beløp per person = \frac{800}{antall personer}

Vi ser at:

2 personer deler: Hver betaler $\frac{800}{2} = 400$ kr
4 personer deler: Hver betaler $\frac{800}{4} = 200$ kr
8 personer deler: Hver betaler $\frac{800}{8} = 100$ kr
16 personer deler: Hver betaler $\frac{800}{16} = 50$ kr

Vi ser at når antallet personer dobles, så halveres beløpet per person. Produktet er alltid konstant:

2 \cdot 400 = 4 \cdot 200 = 8 \cdot 100 = 16 \cdot 50 = 800

Dette er typisk for omvendt proporsjonale størrelser.

Oppsummering:

Proporsjonale størrelser: Når den ene øker, øker den andre på samme måte. Grafen er en rett linje gjennom origo. Eksempel: Hvis hver kule koster 20 kr, er antall kuler og total kulepris proporsjonale.
Omvendt proporsjonale størrelser: Når den ene øker, minker den andre slik at produktet er konstant. Grafen er en hyperbel. Eksempel: Beløpet per person og antall personer som deler er omvendt proporsjonale.