Jeg blir veldig glad om du melder ifra om feil enten direkte til meg eller via forumet på matematikk.net.
Oppgave 1-1
Siden 88 % har svart, så må de gjenværende 12 prosentene tilsvare de 3 elevene. Vi kan gå veien om en ved å finne ut hvor mange elever 1 prosent tilsvarer.
1 % tilsvarer altså 0,25 elever, og dermed tilsvarer 100 % 25 elever.
Det er 25 elever i klassen.
Oppgave 1-2
1-2a
Medianen er det midterste tallet etter at vi har sortert dem stigende
Siden både 4 og 6 står i midten så er medianen 5.
Gjennomsnittet er summen av tallene delt på antallet observasjoner.
Medianen er 5 og gjennomsnittet er 5.
1-2b
Den kumulative frekvensen for 6 personer er antallet observasjoner som er 6 eller mindre. Det er 7 av de 10 observasjonene som er på 6 personer eller mindre.
Den kumulative frekvensen for 6 personer er 7, det betyr at det i 7 av de 10 tilfellene var 6 personer eller færre i vogna i skiheisen.
Oppgave 1-3
1-3a
Jeg ser at dette er en omvendt proporsjonal funksjon siden en dobling fra 2 til 4 deltakere gir en halvering av prisen per elev fra 4000 kr til 2000 kr.
Siden det koster 800 kr per person hvis de er 10 elever må det koste 400 kr per person dersom de er 20 elever.
Det koster 400 kr per person dersom det er 20 elever på festen.
1-3b
Funksjonsuttrykkene for omvendt proporsjonale er på formen
Der
Oppgave 1-4
Høyre sin framgang var fra 24 % til 28 %, det gir en prosentvis framgang på
Fremskrittspartiet sin framgang var fra 16 % til 20 %, det gir en prosentvis framgang på
Siden
Det er mulig at man kan få full uttelling (1 poeng) ved å argumentere for 4 prosentpoeng vil være mye mer verdt for et lite parti enn et stort parti (uten å gjøre beregninger). Hvis beregningene ovenfor er vanskelig så anbefaler jeg at du heller lager et enklere eksempel enn oppgaveteksten inneholder. Hvis du heller velger å sammenligne et parti som har 4 % og som får 4 prosentpoeng økning mot et parti som har 8 % og får 4 prosentpoeng økning, så får du mye enklere regnestykker. Da vil du ha gjort beregninger som viser at argumentet om at 4 prosentpoeng er «mest verdt» for et lite parti stemmer.
Oppgave 1-5
Vi ser et regnestykke med differansen mellom to ulike ledd. For at svaret skal bli størst mulig må det første leddet være så stort som mulig, og det andre leddet (det vi trekker fra) må være så lite som mulig.
Siden potenser blir veldig store når eksponentene er høye så vil
Oppgave 1-6
1-6a
Her kan man tegne opp de neste kvadratene for å vise hvordan man finner svaret, eller så må man beskrive mønsteret eller finne formelen.
Jeg velger å beskrive mønsteret ved å sette opp en oversikt.
Jeg ser at hele figuren er rektangler som øker med 2 i bredden og 1 i høyden for hver figur. De hvite feltene øker med 3 for hver figur. Jeg setter opp en oversikt.
| Figurnummer | Antall totalt | Antall hvite | Antall grønne |
|---|---|---|---|
| 1 | 1 | 8 | |
| 2 | 4 | 16 | |
| 3 | 7 | 28 | |
| 4 | 10 | 44 | |
| 5 | 13 | 64 |
Det er 64 grønne ruter i figur 5.
1-6b
Antallet hvite kvadrater øker med 3 for hver figur, og det starter på 1.
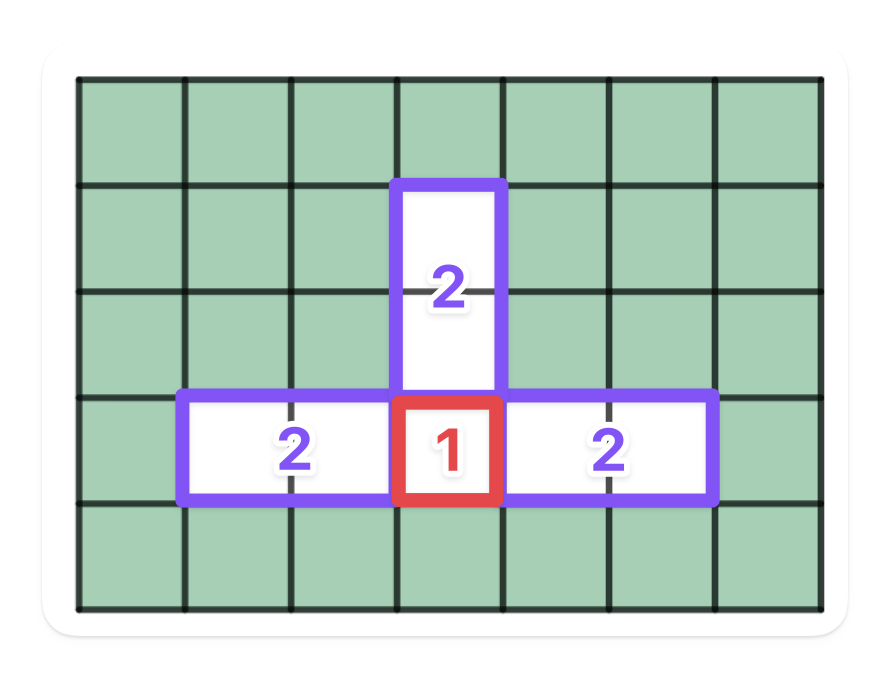
I figuren over har jeg delt opp figur nr 3 i 4 ulike deler. Jeg ser at vi har tre like deler med lengde 2 merket med lilla farge. Disse er altså 1 mindre enn figurtallet. I tillegg har vi en ekstra hvit rute som er fast i alle figurene, merket med rød farge. For figur 3 kunne vi altså skrevet opp antallet som
1-6c
Jeg har allerede sett at det er mulig å finne størrelsen av hele rektangelet og trekke fra de hvite feltene for å finne ut hvor mange grønne ruter det er. Det store rektangelet øker med 2 i bredden og 1 i høyden, og vi ser at bredden er
For å finne antallet grønne ruter så kan vi trekke fra antallet hvite ruter.
I figur nummer
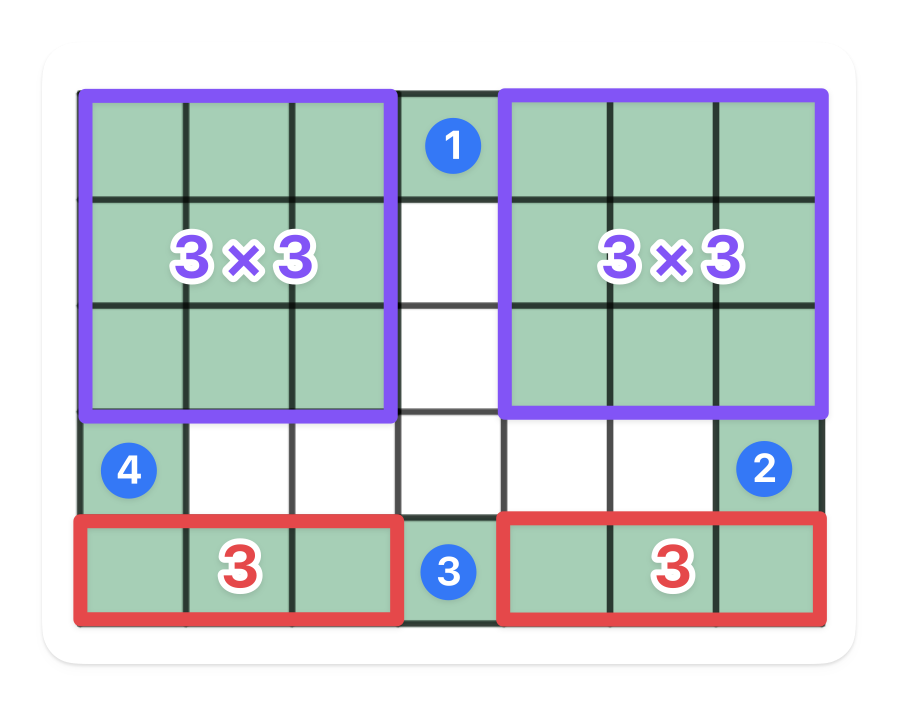
Vi kunne også funnet formelen for antallet grønne felter ved å dele opp de grønne feltene i mindre deler, se figuren.
Oppgave 1-7
Trine må ha antatt at det er omtrent like mange personer i hver alder i hver klasse, altså at det for eksempel er 5 16-åringer, 5 17-åringer, 5 18-årnger og 5 19-åringer i den første klassen.
Hvis den antakelsen stemmer så kan vi finne gjennomsnittsalder ved å ta klassemidtpunktet for hver klasse og multiplisere med antallet medlemmer i klassen.
| Alder | Midtpunkt | Frekvens | Midtpunkt |
|---|---|---|---|
| 18 | 20 | 360 | |
| 30 | 40 | 1200 | |
| 50 | 30 | 1500 | |
| 75 | 10 | 750 | |
| Sum | 100 | 3810 |
Gjennomsnittsalderen er omtrent
Medianen er «den midterste personen» blant de 100 hvis vi sorterer dem etter alder. Altså vil medianen være gjennomsnittet av alderen til person nr. 50 og 51.
Vi tenker oss de 100 personene sortert etter alder i en lang rekke. De 20 yngste personene er under 20 år. I den neste klassen er det 40 personer, og medianpersonen vil være gjennomsnittet av person nr. 30 og 31 inni denne klassen.
Hvis vi fordeler personene i klassen
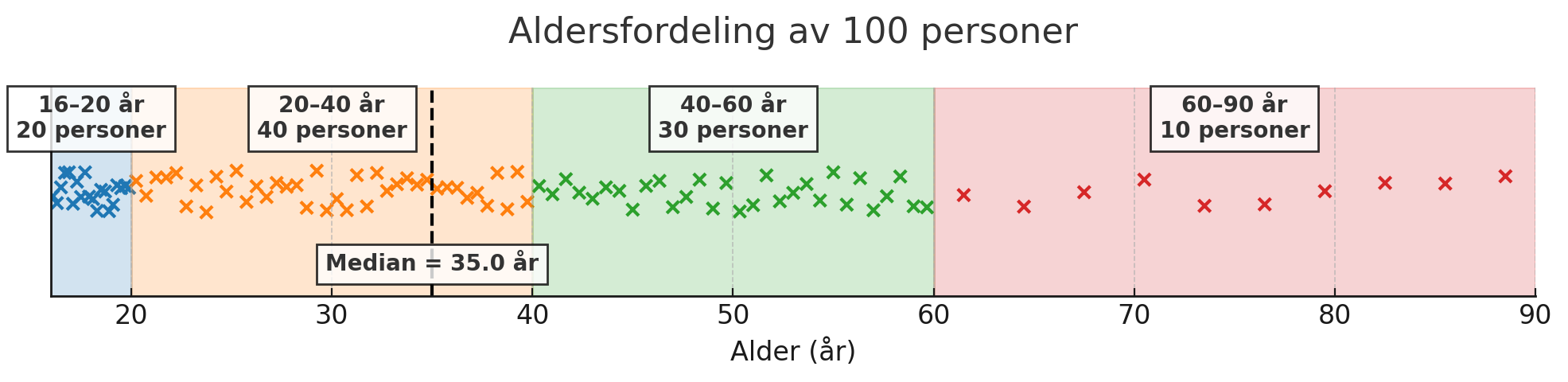
Gjennomsnittet er ca. 38 år og medianalderen er ca. 35 år hvis personene er jevnt fordelt innenfor hver klasse.
I dette diagrammet har jeg forsøkt å vise aldersfordelingen. Hvert kryss er en person. Personene er jevnt fordelt innenfor hver klasse, slik som Trine må ha antatt.
Oppgave 1-8
I programmet ser jeg følgende:
- Linje 1: matsvinnet starter på 160 kg
- Linje 2: Målet er å halvere matsvinnet til 80 kg
- Linje 3: Vekstfaktoren er 0,87, altså 13 % nedgang.
- Linje 7: Starter en løkke som kjører fram til matsvinnet er mindre enn målet vårt på 80 kg
- Linje 8: Reduserer matsvinnet med 13 %
- Linje 9: Beregner hvilket år vi er i
Sofie ønsker å finne ut hvor mange år det tar før vi har halvert matsvinnet vårt.
Verdiene som skrives ut forteller at vi når målet i 2030 dersom vi reduserer med 13 % per år, og at utslippet da vil være 79,7 kg per familie på fire.
Oppgave 2-1
2-1a
er en eksponentialfunksjon som synker med 5 % for hvert år. Dette viser at prosessen som i dag slipper ut 5000 tonn per år kommer til å reduseres med 5 %. er en konstant funksjon, denne verdiene endrer seg altså ikke i framtiden. Dette viser at prosessen som i dag slipper ut 1000 tonn per år kommer til å fortsette på samme måte i framtiden.
Ledelsen ønsker å minke utslippet fra den ene prosessen med 5 % per år, og ikke gjøre noe med den andre prosessen.
2-1b
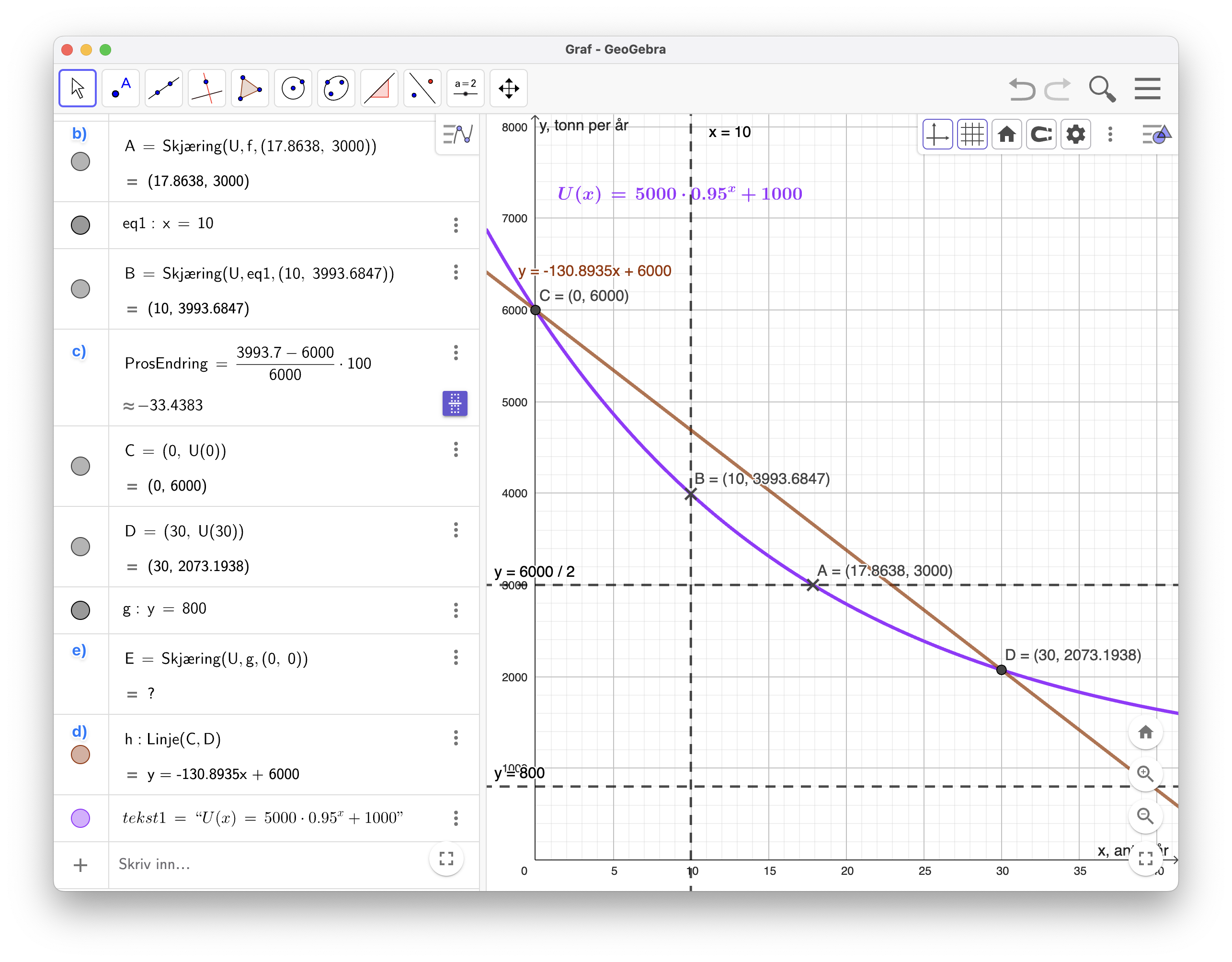
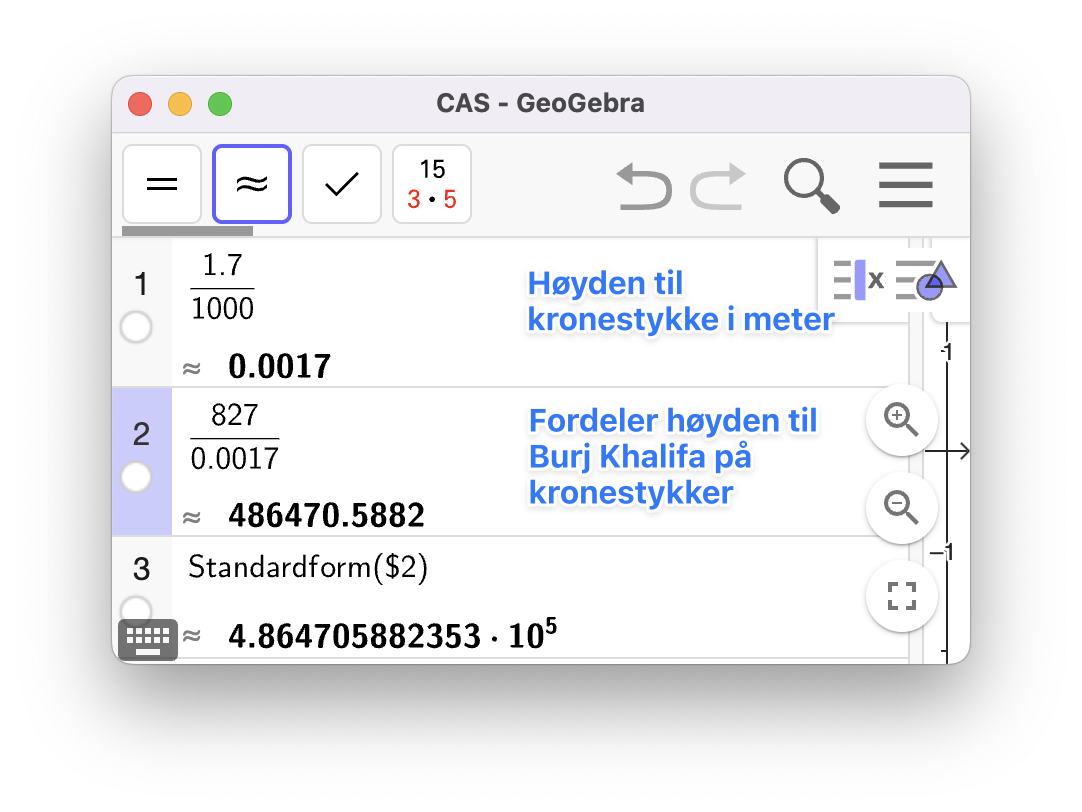
Til de neste oppgavene har jeg brukt GeoGebra til å regne ut svarene, se figuren-1.
For å finne antall år før utslippene blir halvert har jeg lagt ut linja
Utslippene vil være halvert til 3000 tonn per år etter 18 år.
2-1c
For å finne utslippet etter 10 år har jeg lagt ut linja
Jeg har beregnet den prosentvise endringen i algebrafeltet, se linjen merket c) ProsEndring.
Utslippene har minket med 33,4 % etter 10 år.
2-1d
Jeg la ut punktene
Stigningstallet til linja er omtrent -131, dette betyr at utslippene i gjennomsnitt minker med 131 tonn per år hvert år i løpet av de 30 første årene.
2-1e
Jeg sjekket dette ved å lete etter skjæringen i mellom Udefinert siden disse funksjonene ikke skjærer hverandre. Dette kunne jeg også sett fra funksjonsuttrykket med leddet
Det er ikke mulig å komme ned til 800 tonn per år med dagens modell.
Oppgave 2-2
Se utklippet over.
Du vil trenge omtrent
Oppgave 2-3
2-3a
Akkurat nå er det 10 personer i rommet. Medianalderen blir da gjennomsnittet av aldrene til person nummer 5 og 6. Denne medianalderen er foreløpig
Dersom det kommer en ellevte person inn så er det person nr. 6 som vil være medianalderen:
- Hvis personen er yngre enn 29 år så vil medianalderen bli 28
- Hvis personen er eldre enn 29 år så vil medianalderen bli 30
- Hvis personen er 29 år så blir den nye medianalderen 29
Påstanden er riktig.
2-3b
Hvis det kommer en ny person inn i rommet så blir det 11 personer i rommet. Hvis deres gjennomsnittsalder skal være 30 så må summen av alle aldrene være
Foreløpig er summen av aldrene 313 år. Hvis den siste personen er 17 år så blir blir summen 330 år, og dermed blir gjennomsnittet
Påstanden er riktig.
Oppgave 2-4
Hvis pris og mengde skal være proporsjonale størrelser så må det være en fast pris per liter eller milliliter med antibac.
For den ene flasken er prisen per milliliter
De andre flaskene må da koste
Den lille flasken må koste 19 kr og den store flasken må koste 760 kr for at prisene og mengde skal være proporsjonale størrelser.
Oppgave 2-5
2-5a
For at skjerfet skal øke med like mange centimeter per uke, så må vi bruke en lineær modell på formen
Vi vet at skjerfet er 8 m i dag, og at det skal bli 40 meter etter 25 uker. Det skal altså øke med vekstfarten
En lineær modell for lengden på skjerfet etter
Denne oppgaven kan løses med lineær regresjon i GeoGebra med punktene
2-5b
Jeg løser oppgaven i CAS. Vi skal finne ut når funksjonen vår passerer 17 m, vi skal altså løse likningen

Det tar 7 uker før skjerfet er 17 meter langt ifølge modellen.
Vi kan tegne funksjonen i GeoGebra og finne skjæringen med linja
Oppgave 2-6
2-6a
Jeg bruker regresjon for å vise dette, se figuren.
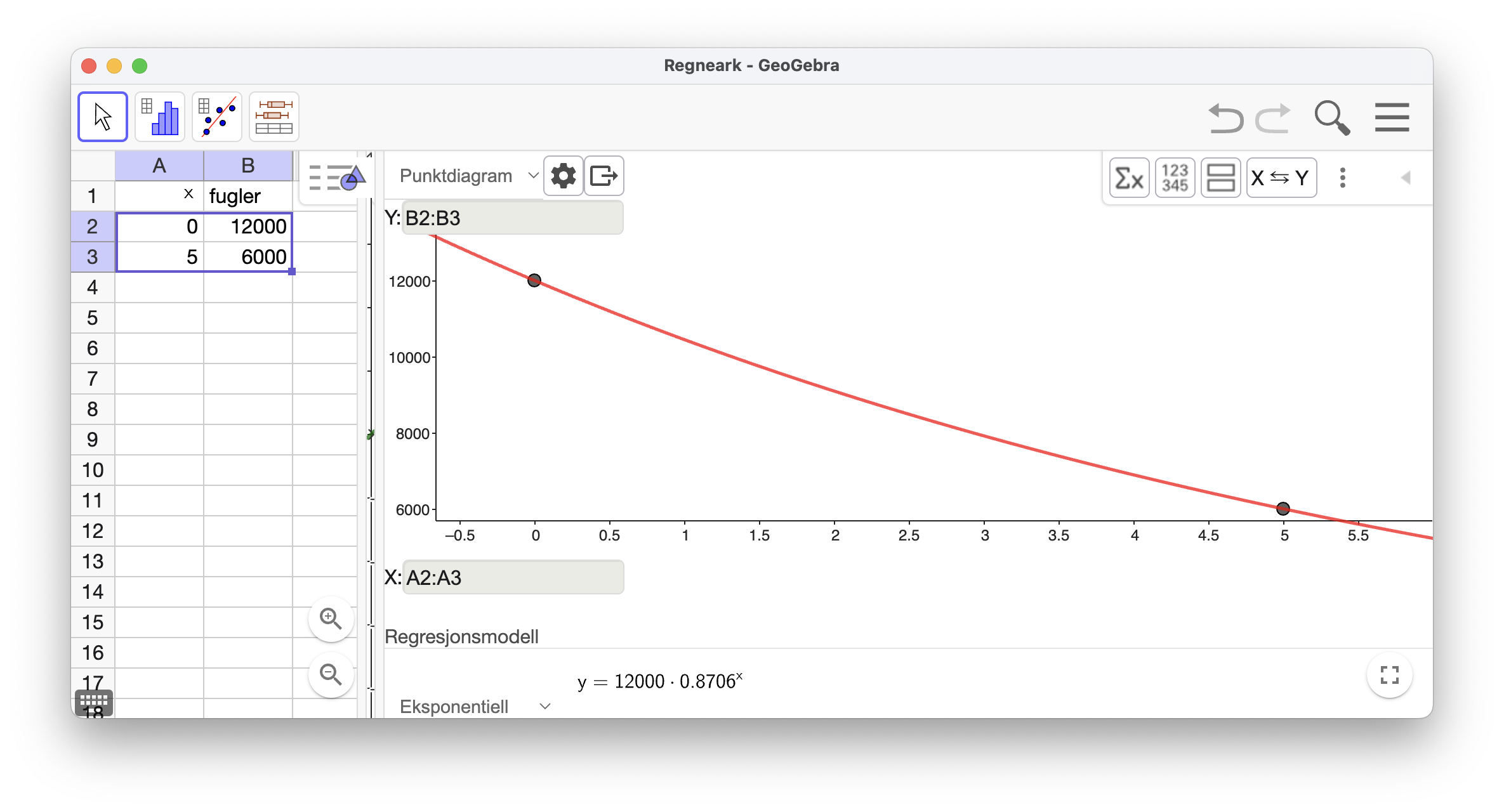
Funksjonen
2-6b
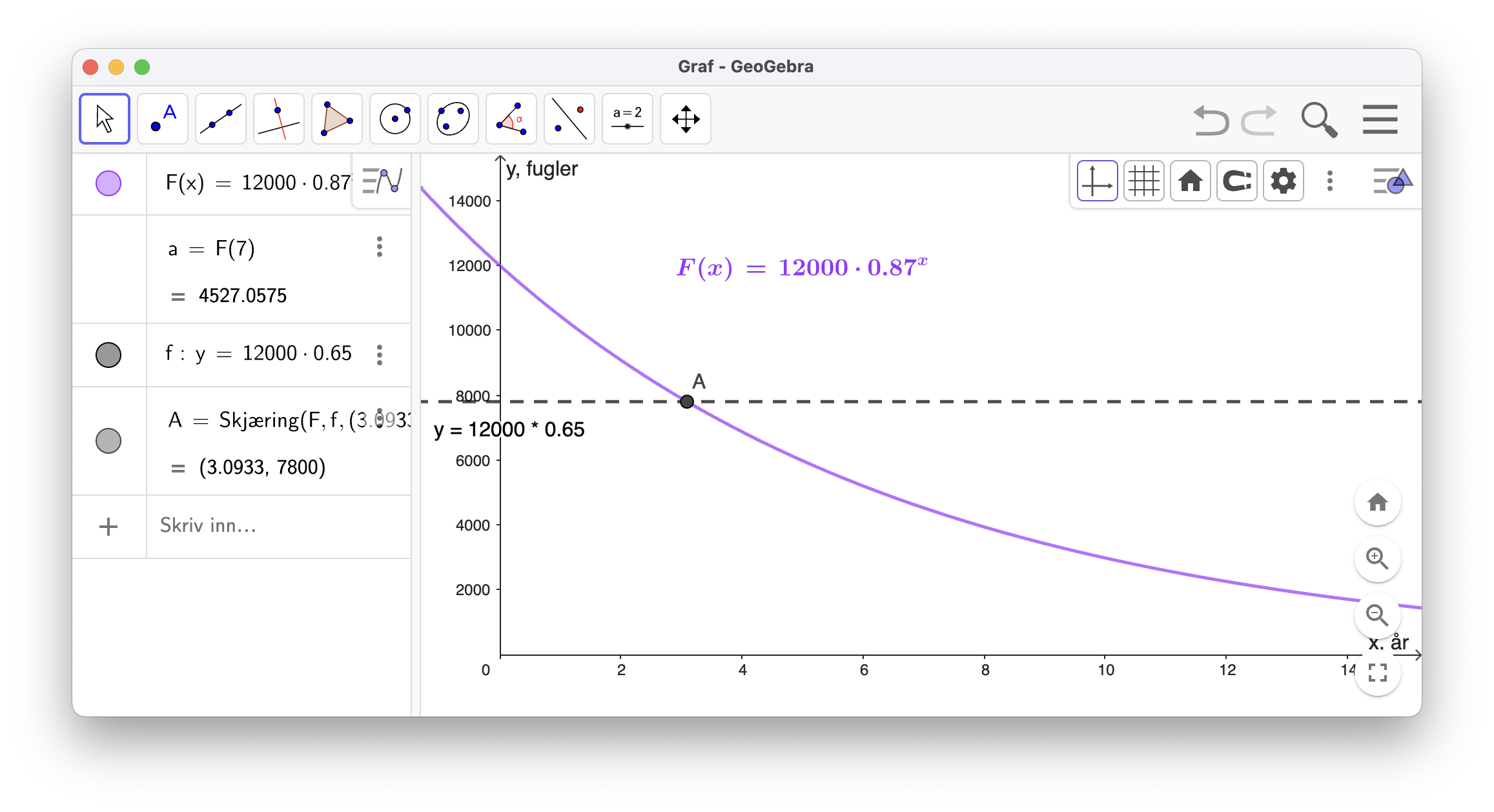
Jeg sjekket verdien av
Etter 7 år vil det være 4527 fugler ifølge modellen.
2-6c
Når bestanden er redusert med 35 % er det 65 % igjen, altså
Det tar 3 år før bestanden er redusert med 35 % ifølge modellen.
Oppgave 2-7
Figuren viser et eksempel på svar på denne oppgaven, hvor jeg viser ulike framstillinger og beregninger.
Siden vi skal skal vise utvikling over tid fra 1983 til 2023 så passer linjediagrammer best. Jeg lager tre ulike linjediagrammer, ett diagram som passer til hver måleenhet (antall, antall per 1000 og antall per kvinne). For å vise beregninger med prosentvise endringer så har jeg laget en tabell som viser prosentvis endring fra 1983 fram til hvert år, og jeg har også vist formlene for beregningene i presentasjonen.
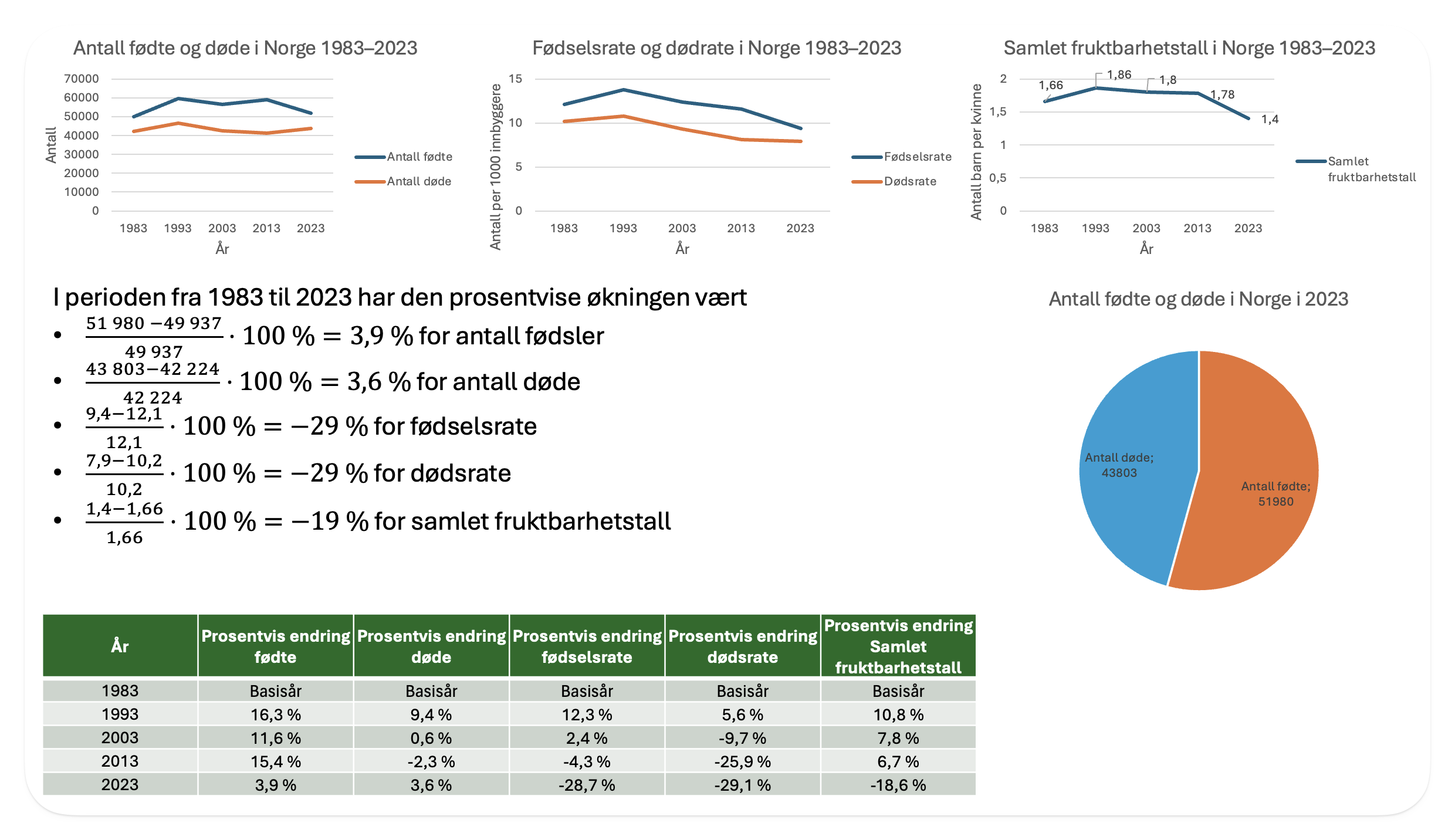
Dette er en type oppgave som har mange ulike svar, og det er vanskelig å si nøyaktig hva som er nok for å få full uttelling (4 poeng) på denne oppgaven. Fjorårets sensorveiledning sa at besvarelsene skulle vurderes på følgende måte
For å få full uttelling må kandidaten gjøre relevante sammenlikninger og beregninger og lage ulike diagrammer som illustrerer opplysningene på en god måte. Det er viktig at sensor ser på helheten i besvarelsen, vurder om informasjonen som presenteres er riktig og relevant, og om diagrammene illustrerer hele eller deler av datamaterialet på ulike måter.
Sensor skal også vurdere kandidatens digitale kompetanse, dvs. valg av egnede diagramtyper, og hvor tydelig informasjonen kommer fram i hvert diagram (bruk av overskrifter, aksetitler, dataetiketter osv.) Som et utgangspunkt kan de 4 poengene uttrykke høy måloppnåelse (4 poeng), middels måloppnåelse (2 - 3 poeng) og lav måloppnåelse (1 poeng).
Jeg synes det er vanskelig å tolke fra oppgaveteksten om det er tilstrekkelig å bare ha med diagrammer som illustrerer utviklingen og beregningen som viser prosentvise endringer, eller om vi skal skal ta med enda flere relevante sammenligninger og beregninger.