Løsningsforslag S2 eksamen H2024

Jeg blir veldig glad om du melder ifra om feil enten direkte til meg eller via forumet på matematikk.net.

Oppgave 1-1

1-1a

Siden vi skal regne ut integralet til produktet av to ulike funksjoner vil jeg forsøke delvis integrasjon. Jeg benytter DI-metoden, og velger at $x^{2}$ er den faktoren som skal integreres, og $\ln x$ er faktoren som skal deriveres.

Hvordan velge hva som skal deriveres og integreres

I lignende oppgaver har vi ofte valgt å derivere den faktoren som er et polynomuttrykk, slik at faktoren blir null etter at vi har derivert en eller flere ganger. I dette tilfellet er det likevel lurt å velge å integrere polynomfaktoren, siden $\ln x$ er litt vanskelig å integrere. I tillegg ser vi et veldig flott mønster med at $(\ln x)^{'} = \frac{1}{x}$ og vi dermed får en rad i DI-systemet som vi kan integrere produktet av.

	D	I
$+$	$\ln x$	$x^{2}$
$-$	$\frac{1}{x}$	$\frac{1}{3} x^{3}$

Vi ser at produktet i rad 2 er $\frac{1}{x} \cdot \frac{1}{3} x^{3}$ , som vi kan integrere.

Vi kan altså sette opp

\begin{aligned} \int x^{2} \ln x d x & = \ln x \cdot \frac{1}{3} x^{3} - \int \frac{1}{x} \cdot \frac{1}{3} x^{3} d x \\ = \frac{1}{3} x^{3} \ln x - \frac{1}{3} \int x^{2} d x \\ = \frac{1}{3} x^{3} \ln x - \frac{1}{3} \cdot \frac{1}{3} x^{3} + C \\ = \underset{―}{\underset{―}{\frac{1}{3} x^{3} (\ln x - \frac{1}{3}) + C}} \end{aligned}

1-1b

Vi setter opp likningen og løser

\begin{aligned} \int_{- 1}^{x} (3 t^{2} - 1) d t & = 0 \\ {[t^{3} - t]}_{- 1}^{x} & = 0 \\ (x^{3} - x) - ((- 1)^{3} - (- 1)) & = 0 \\ (x^{3} - x) - (- 1 + 1) & = 0 \\ (x^{3} - x) - 0 & = 0 \\ x^{3} - x & = 0 \\ x (x^{2} - 1) & = 0 \end{aligned}

Denne likningen har tre løsninger: $x = 0 \lor x = - 1 \lor x = 1$ . Vi forkaster løsningen $x = - 1$ siden vi har fått oppgitt at $x > - 1$ i oppgaveteksten.

\underset{―}{\underset{―}{x = 0 \lor x = 1}}

1-1c

La $f (t) = 3 t^{2} - 1$ .

I b)-oppgaven fant vi blant annet ut at

\int_{- 1}^{0} (3 t^{2} - 1) d t = 0

Det betyr at området avgrenset av grafen til $f$ , linja $x = - 1$ , linja $x = 0$ og $x$ -aksen må bestå av like store områder over $x$ -aksen og under $x$ -aksen.

Vi fant også ut at $\int_{- 1}^{1} f (t) d t = 0$ . På samme måte betyr dette at området avgrenset av grafen til $f$ , linja $x = - 1$ , linja $x = 1$ og $x$ -aksen må bestå av like store områder over $x$ -aksen og under $x$ -aksen.

Oppgave 1-2

1-2a

Summen av en aritmetisk rekke er gitt ved

s_{n} = \frac{a_{1} + a_{n}}{2} \cdot n

Vi ser at differansen $d = 4$ . For å finne ut hvor mange ledd det er i rekka vår kan vi løse

3 + (n - 1) \cdot 4 = 399 ⟹ n - 1 = \frac{399 - 3}{4} ⟹ n = 100

Summen av de 100 første leddene blir altså

s_{100} = \frac{3 + 399}{2} \cdot 100 = \frac{402}{2} \cdot 100 = 201 \cdot 100 = \underset{―}{\underset{―}{20 100}}

1-2b

Vi vet at summen av en uendelig geometrisk rekke som konvergerer er

s = \frac{a_{1}}{1 - k} ⟺ 1 - k = \frac{a_{1}}{s} ⟺ k = 1 - \frac{a_{1}}{s}

Vi setter inn verdiene i uttrykket for $k$

k = 1 - \frac{12}{18} = 1 - \frac{2}{3} = \underset{―}{\underset{―}{\frac{1}{3}}}

1-2c

Vi kan omskrive tallet som summen av en uendelig rekke med ledd på denne måten $0,757 57575 \dots = 0, 75 + 0,007 5 + 0,000 075 + \dots$

Hvert av disse leddene kan vi skrive om som brøker

\begin{aligned} 0, 75 & = \frac{3}{4} \\ 0,007 5 & = \frac{\frac{3}{4}}{100} = \frac{3}{400} \\ 0,000 075 & = \frac{\frac{3}{4}}{10000} = \frac{3}{40000} \end{aligned}

Vi ser et mønster hvor hvert ledd er $\frac{1}{100}$ av det forrige, altså har vi

\frac{3}{4} + \frac{3}{400} + \frac{3}{40000} + \dots = \frac{3}{4 \cdot 100^{0}} + \frac{3}{4 \cdot 100^{1}} + \frac{3}{4 \cdot 100^{2}} + \dots

Vi har altså vist at $0,757 57575 \dots$ kan skrives som en uendelig geometrisk rekke, og med sumnotasjon blir rekka

lim_{n \to \infty} \sum_{i = 1}^{n} \frac{3}{4 \cdot 100^{i - 1}} = 0,757 57575 \dots

Denne uendelig geometrisk rekka har $a_{1} = \frac{3}{4}$ og $k = \frac{1}{100}$ . Summen av rekka er gitt ved

s = \frac{\frac{3}{4}}{1 - \frac{1}{100}} = \frac{\frac{3}{4}}{\frac{99}{100}} = \frac{300}{396} = \frac{75}{99} = \frac{25}{33}

Siden vi nå vet at $0,757 57575 + \dots = \frac{25}{33}$ så kan vi vise følgende

1,757 57575 \dots = 1 + 0,757 57575 \dots = 1 + \frac{25}{33} = \frac{58}{33}

Vi har altså vist at $1,757 57575 \dots = \underset{―}{\underset{―}{\frac{58}{33}}}$ .

Oppgave 1-3

Tabell: Sannsynlighetsfordelingen til oppgave 1-3

$x$	0	1	4	$b$
$P (X = x)$	$0, 30$	$0, 40$	$0, 10$	$0, 20$
$x \cdot P (X = x)$	$0$	$0, 40$	$0, 40$	$0, 20 \cdot b$
$(x - μ)^{2}$	$(- 2)^{2} = 4$	$1^{2} = 1$	$2^{2} = 4$	$4^{2} = 16$
$(x - μ)^{2} \cdot P (X = x)$	$4 \cdot 0, 30 = 1, 2$	$1 \cdot 0, 40 = 0, 40$	$4 \cdot 0, 10 = 0, 40$	$16 \cdot 0, 20 = 3, 2$

Vi vet at forventningsverdien er summen av produktene av $x \cdot P (X = x)$ , se rad 2 i tabellen. Det betyr at

0 + 0, 40 + 0, 40 + 0, 20 b = 2 ⟺ 0, 20 b = 1, 2 ⟺ b = 6

Vi har vist at $\underset{―}{\underset{―}{b = 6}}$ .

Variansen til $X$ er gitt ved

\begin{aligned} Var (X) & = \sum_{i = 1}^{N} ((x_{i} - μ)^{2} \cdot P (X = x_{i})) \\ Var (X) & = 1, 2 + 0, 40 + 0, 40 + 3, 2 = \underset{―}{\underset{―}{5, 2}} \end{aligned}

Variansen $\underset{―}{\underset{―}{Var (X) = 5, 2}}$ .

Oppgave 1-4

1-4a

Vi kan bruke en binomisk sannsynlighetsmodell siden vi kan regne dette som 1000 uavhengige forsøk hvor frøene enten spirer eller ikke spirer. På grunn av sentralgrensesetningen kan vi også bruke normalfordeling som en tilnærming til den binomiske fordelingen.

Var (X) = n p (1 - p) = 1000 \cdot 0, 7 \cdot 0, 3 = 210

I dette tilfellet er normalfordelingen en svært god tilnærming til den binomiske fordelingen siden variansen er mye større enn 5.

Vi bestemmer forventningsverdien og standardavviket

E (X) = μ = n p = 1000 \cdot 0, 7 = 700 og σ = \sqrt{210} \approx 14

Vi vet at omtrent 68 % av utfallene kommer til å havne innenfor ett standardavvik fra forventningsverdien, altså at $P (μ - σ < X < μ + σ) \approx 0, 68$ .

Vi ser at figur 1 må ha et standardavvik på mer enn 100, derfor må figur 2 være riktig figur.

1-4b

Vi kan bruke samme tankegang som i forrige oppgave. Vi ser at figur 4 har mye mer enn 68 % av sitt skraverte areal innenfor intervallet $[μ - σ, μ + σ] = [40, 60]$ .

Figur 3 viser sannsynlighetstettheten.

Oppgave 1-5

1-5a

Vi kan finne grensekostnaden ved å derivere kostnadsfunksjonen

K^{'} (x) = 2 \cdot 0, 3 x + 10 = 0, 6 x + 10

Enhetskostnaden er gitt ved

E (x) = \frac{K (x)}{x} = \frac{0, 3 x^{2} + 10 x + 3000}{x} = 0, 3 x + 10 + \frac{3000}{x}

Vi setter disse lik hverandre

\begin{aligned} K^{'} (x) & = E (x) \\ 0, 6 x + 10 & = 0, 3 x + 10 + \frac{3000}{x} \\ 0, 3 x & = \frac{3000}{x} \\ 0, 3 x^{2} & = 3000 \\ x^{2} & = \frac{3000}{0, 3} \\ x^{2} & = 10 000 \\ x & = 100 \end{aligned}

Vi ser bort fra den negative løsningen av likningen siden vi snakker om produksjon av $x$ enheter.

Grensekostnaden er lik enhetskostnaden ved produksjon av 100 enheter. Dette er også den produksjonsmengden som gir de laveste enhetskostnadene.

1-5b

Inntektene fra salget er gitt ved

I (x) = pris \cdot x = 400 x ⟹ I^{'} (x) = 400

Vi har største overskudd når grensekostnaden er lik grenseinntekten

\begin{aligned} K^{'} (x) & = I^{'} (x) \\ 0, 6 x + 10 & = 400 \\ 0, 6 x & = 390 \\ x & = \frac{390}{0, 6} \\ x & = \frac{3900}{6} \\ x & = 650 \end{aligned}

Bedriften må produsere og selge 650 enheter for at overskuddet skal bli størst mulig.

Oppgave 2-1

2-1a

Jeg la inn dataene i GeoGebra og gjorde en regresjonsanalyse med logistisk modell. Som vi ser fra funksjonen som GeoGebra foreslår, så passer funksjonen $L (t)$ godt til denne situasjonen.

L (t) = \frac{156, 31}{1 + 12, 21 e^{- 0, 24 t}}

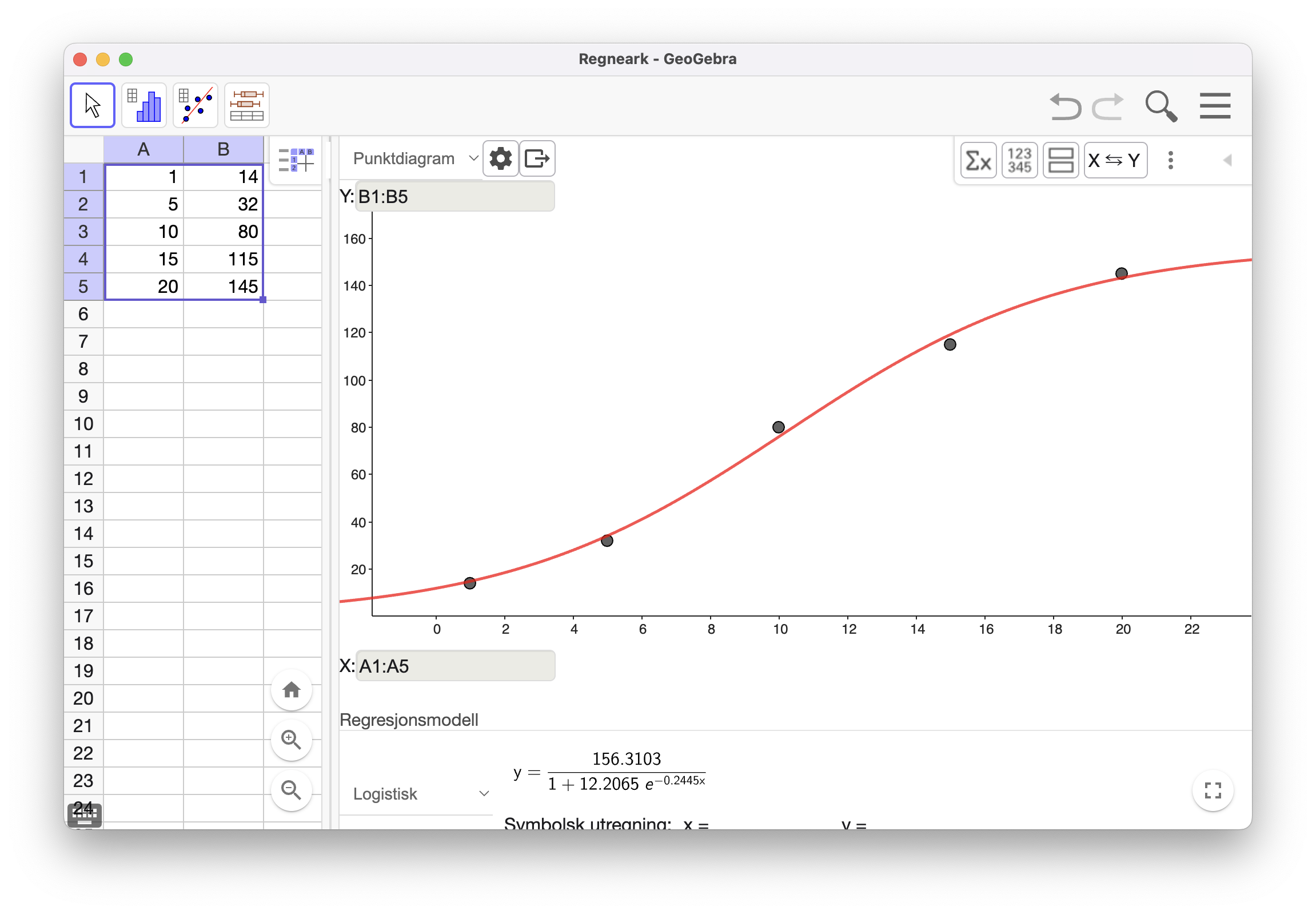
Regresjon av logistisk funksjon i GeoGebra

En logistisk modell vil passe godt for denne typen situasjon, siden veksten vil avta før funksjonen nærmer seg en øvre grense. Den øvre grensen er i dette tilfellet 156,3 km. Det høres ut som en rimelig øvre grense for maratontrening (Jakob Ingebrigtsen, som er verdensmester på 1500 m, trener opp mot 180 km i uka på det meste).

2-1b

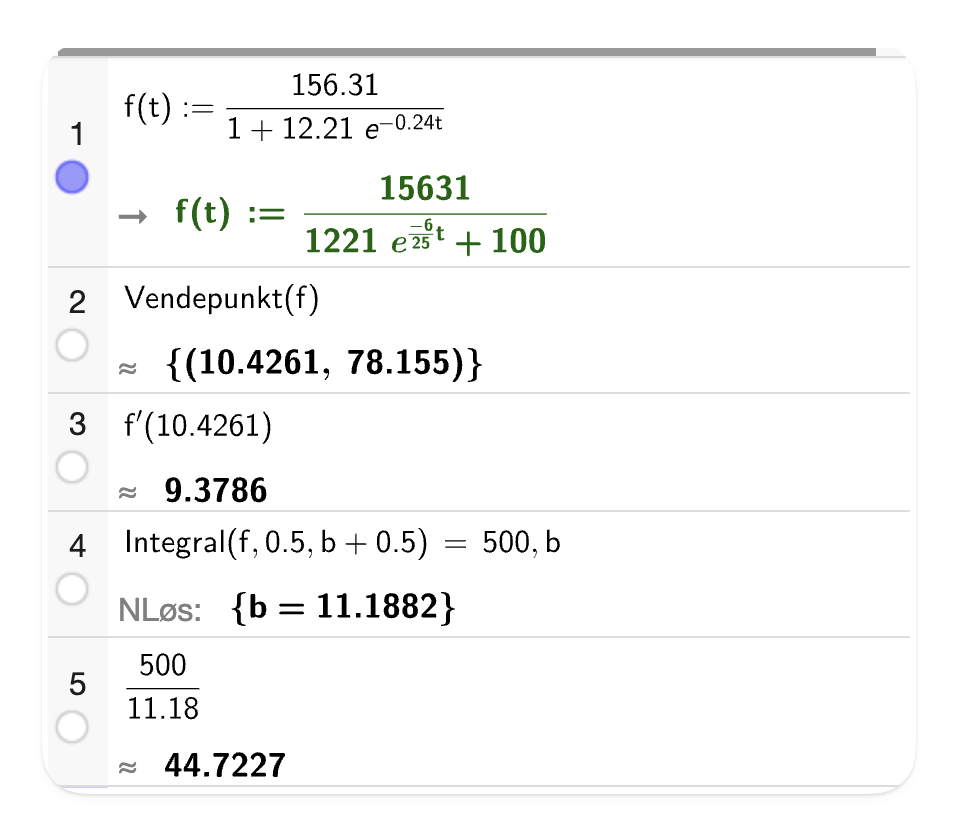
Løsning av oppgave 1a og 1b del 2 i CAS

Vi vet at funksjonen vokser raskest i vendepunktet, så vi finner dette med GeoGebra i linje 2. $t = 10, 43$ tilsvarer at vi er omtrent midtveis i den ellevte uka. Økningen i vendepunktet er det samme som den deriverte til funksjonen i vendepunktet, se linje 3 i GeoGebra.

Antall løpte kilometer øker raskest i den ellevte uka, og økningen er da på omtrent 9,4 km per uke.

2-1c

Vi kan løse denne oppgaven på flere måter, men oppgaveteksten legger på mange måter opp til at vi skal bruke funksjonsuttrykket fra a), og finne ut hvor mange uker det går før arealet under grafen blir 500 km.

Å anta at $L (t)$ har tilnærmet kontinuerlig endring kan være en god tilnærming siden Marco sannsynligvis løper flere ganger i uka,

Vi kan finne en god tilnærming til svaret ved å løse likningen

\int_{0}^{b} L (t) d t = 500

og deretter finne gjennomsnittet ved å dividere 500 km med antall uker $b$ .

Vi kan finne en enda bedre tilnærming til svaret dersom vi forskyver grensene for integrasjonen med 0,5 mot høyre

\int_{0, 5}^{b + 0, 5} L (t) d t = 500

Vi løser likningen i linje 4 i GeoGebra, og finner at det tar omtrent 11,19 uker før Marco har løpt 500 km og kjøper nye sko. I gjennomsnitt har han da løpt 44,7 km i uka, se linje 5.

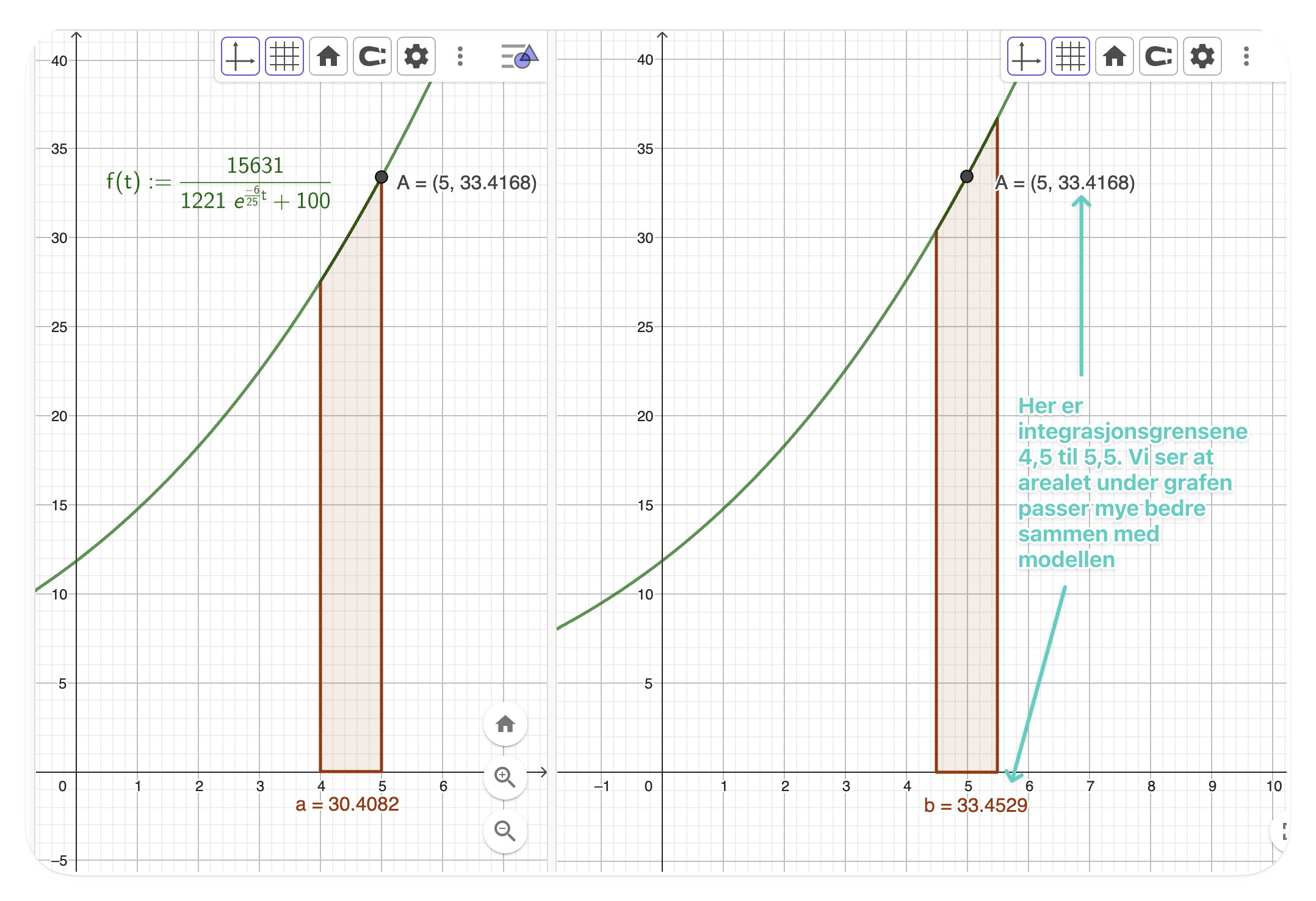
Blir resultatet mer nøyaktig ved å justere grensene i denne oppgaven?

Når vi justerer grensene med $+ 0, 5$ får vi et svar som er omtrent en halv uke mindre enn hvis vi ikke justerer. Det er ikke fryktelig stor forskjell, men det er en forskjell.

Vi kan lage et eksempel for å overbevise oss selv om at det er lurt å justere grensene. La oss se på uke 5. I denne uka har Marco faktisk løpt 32 km, mens den logistiske modellen overestimerer løpslengden og gir $L (5) = 33,417$ .

Hvis vi bruker $\int_{4}^{5} L (t) d t$ for å finne ut hvor langt Marco har løpt i uke 5, så vil alle verdiene for $L (t)$ være lavere enn $L (5)$ siden grafen stiger i hele intervallet. Dermed underestimerer vi Marcos løpsdistanse. Ved å heller flytte grensene til $\int_{4, 5}^{5, 5} L (t) d t$ så vil $L (t) < L (5)$ for $t \in [4, 5, 5 ⟩$ og $L (t) > L (5)$ for $t \in ⟨ 5, 5, 5]$ . Dermed vil underestimeringen i intervallet $t \in [4, 5, 5 ⟩$ «jevnes ut» av overestimeringen i intervallet $t \in ⟨ 5, 5, 5]$ .

Oppgave 2-2

2-2a

Vi har en situasjon hvor vi har to ulike grupper og vi tenker oss at vi skal trekke 20 kandidater tilfeldig blant disse. Vi kan selvsagt ikke trekke den samme kandidaten til intervju 2 ganger, så dette blir en trekning uten tilbakelegging. Derfor passer en hypergeometrisk sannsynnlighetsfordeling godt i dette tilfellet.

Hvis trekningen hadde vært tilfeldig burde sannsynligheten for å trekke en mann på første trekning være $p_{m} = \frac{40}{100} = 0, 4$ . Altså kan vi sette opp følgende hypoteser

\begin{aligned} H_{0} : & p_{m} = 0, 4 \\ H_{1} : & p_{m} > 0, 4 \end{aligned}

Andre hypoteser

Vi kan selvsagt bruke andelen kvinner som utgangspunkt for hypotesene våre. Ved tilfeldig trekning burde sannsynligheten for kvinne på første trekning være $p_{k} = 0, 6$ . Dette gir hypotesene

H_{0} : p_{k} = 0, 6 mot H_{1} : p_{k} < 0, 6

2-2b

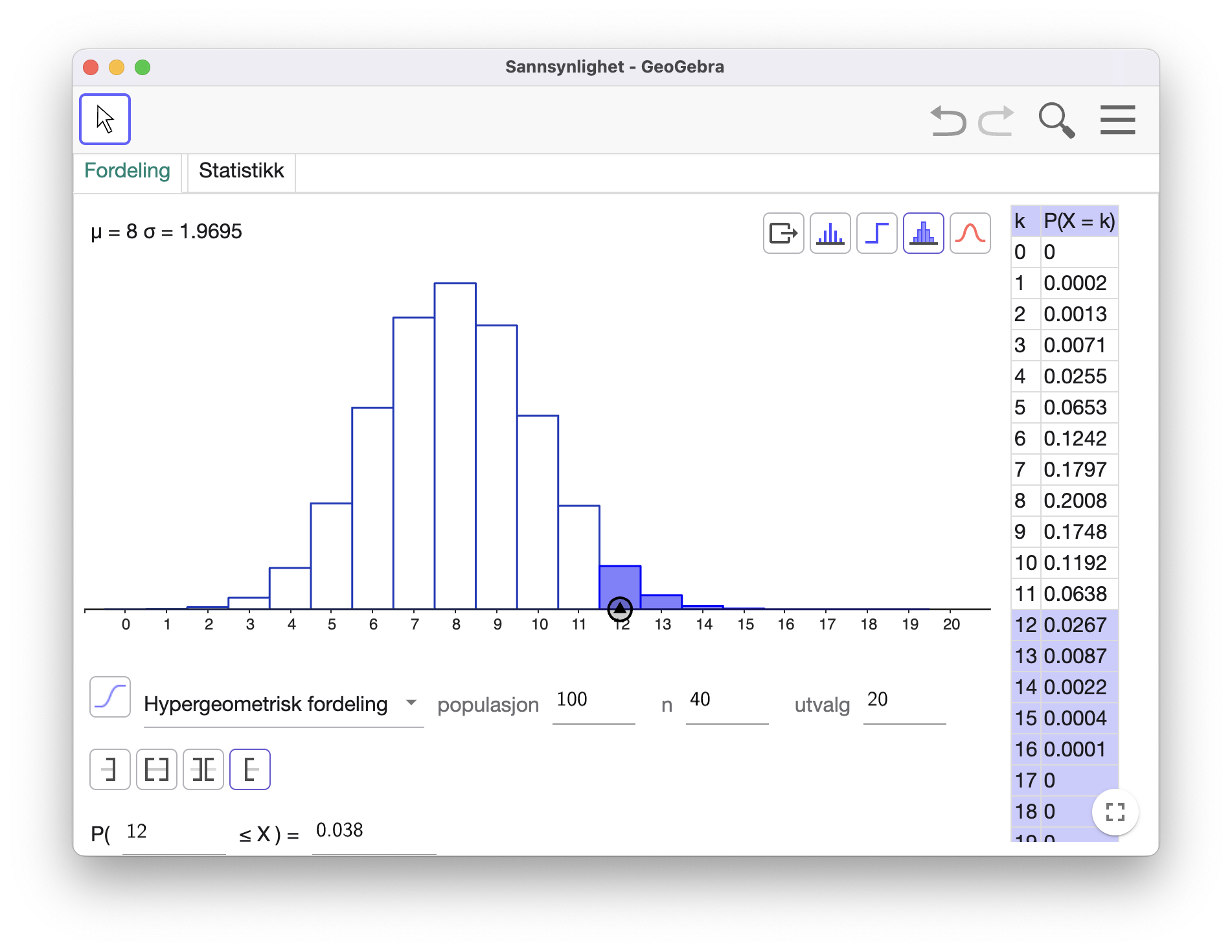
Hypergeometrisk hypotesetest i GeoGebra til oppgave 2-2

I GeoGebra har vi satt opp en hypergeometrisk fordeling med 100 kandidater hvorav 40 er menn. Vi velger 20 tilfeldige kandidater. Sannsynligheten for at minst 12 av disse er menn er $P (X \geq 12) = 0,038$ .

$p$ -verdien på 0,038 er mindre enn signifikansnivået på 5 %, derfor forkaster vi nullhypotesen.

En hypotesetest med signifikansnivå 5 % gir grunnlag for å si at bedriften bevisst velger menn foran kvinner.

Oppgave 2-3

2-3a

Jeg vet at summen av en uendelig geometrisk rekke er gitt ved

s = \frac{a_{1}}{1 - k}

dersom $- 1 < k < 1$ .

Hvis vi vi lar $x = \frac{1}{e}$ så vil rekka bli

1 + (\ln \frac{1}{e} - 1) + {(\ln \frac{1}{e} - 1)}^{2} + \dots

La oss se hva $\ln \frac{1}{e} - 1$ blir

\ln \frac{1}{e} - 1 = \ln 1 - \ln e - 1 = 0 - 1 - 1 = - 2

Det første leddet i rekka er $a_{1} = 1$ og det andre leddet er $a_{2} = - 2$ , det vil si at

k = \frac{- 2}{1} = - 2

$k$ ligger ikke i intervallet $⟨ - 1, 1 ⟩$ , og dermed konvergerer ikke rekka.

Påstanden er usann, rekka konvergerer ikke når $x = \frac{1}{e}$ .

2-3b

$f$ og $g$ kommer til å avgrense maksimalt 2 områder siden $f$ er en tredjegradsfunksjon og $g$ er en andregradsfunksjon. For å finne disse to områdene må vi først finne skjæringspunktene mellom grafene.

Bestemmelse av skjæringspunktet mellom funksjoner i CAS

Jeg fant skjæringspunktene i GeoGebra. (Vi ser her at kravet om at $a > - 1$ gjør at vi får reelle løsninger).

La oss undersøke arealet av områdene som er avgrenset. Jeg gjør dette i GeoGebra ved å integrere fra skjæringspunkt til skjæringspunkt ved hjelp av IntegralMellom.

Bestemmelse av arealet mellom grafene

Påstanden stemmer. Vi ser at arealene mellom grafene er like store.

Oppgave 2-4

2-4a

Jeg setter opp tallene i følgen og sjekker differansene mellom hvert ledd (det er alltid et godt tips for å finne mønstre!). Jeg fant ut at differansene mellom tallene var 1, 4, 9, 16, 25, og disse tallene kjenner jeg igjen som kvadrattallene.

Jeg sjekker om jeg finner en god sammenheng for et av leddene

a_{5} = 31 = 15 + 16 = 15 + 4^{2} = a_{4} + 4^{2}

Jeg ser at jeg kan generalisere denne sammenhengen som

\underset{―}{\underset{―}{a_{n + 1} = a_{n} + n^{2}}}

Alternative rekursive sammenhenger

Det finnes også andre rekursive sammenhenger som som gir samme rekke:

$a_{n} = a_{n - 1} + (n - 1)^{2}$ er den samme sammenhengen som vi nettopp fant, men den gjelder for $n \geq 2$
$a_{n} = {(\sqrt{a_{n - 1} - a_{n - 2}} + 1)}^{2} + a_{n - 1}$ er en sammenheng som ikke bruker $n$ , slik at du ikke er avhengig av å kjenne til hvor i rekka du befinner deg når du bruker formelen

2-4b

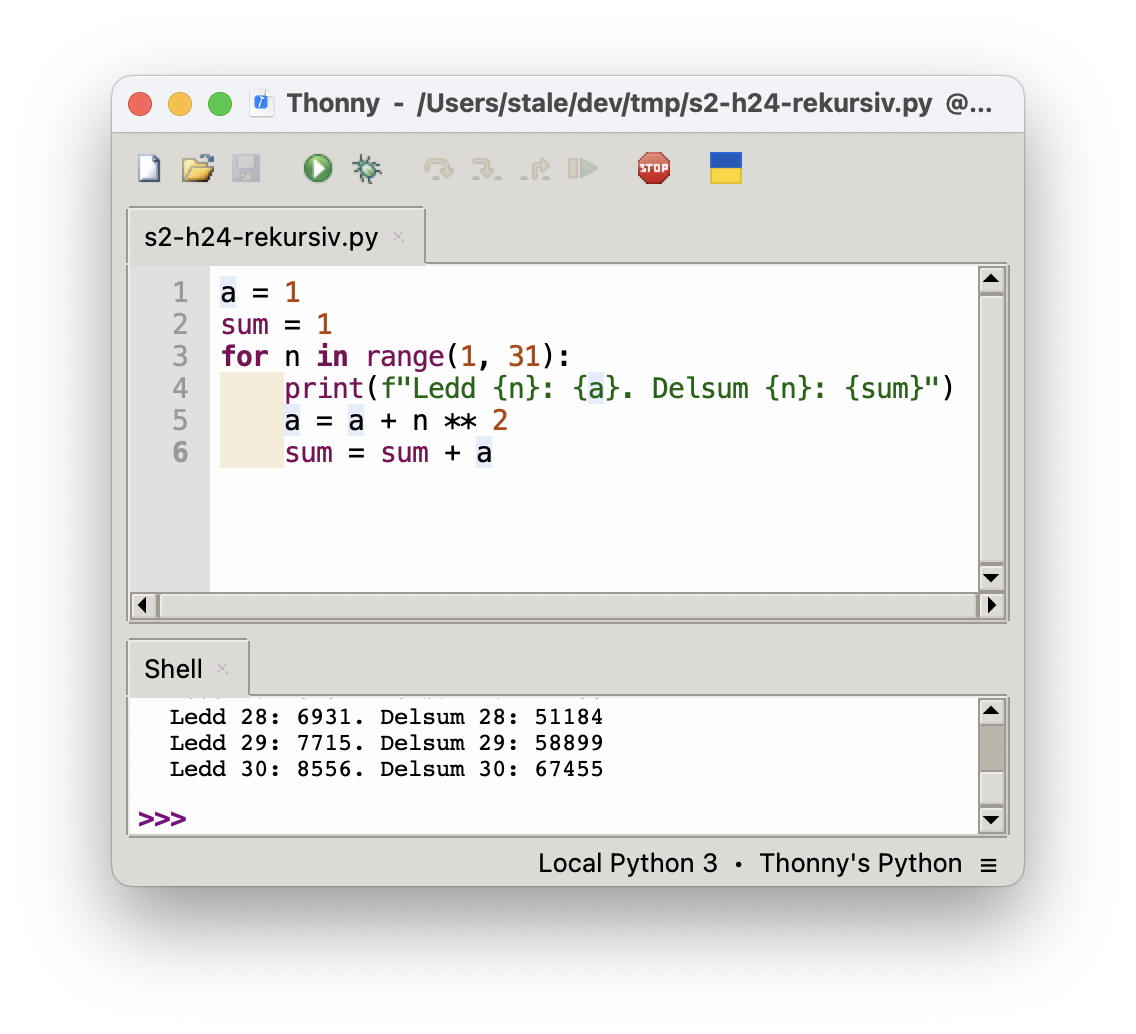
Program for å regne ut ledd i rekke

Jeg brukte en for-løkke til å regne meg fram til delsummen til ledd nummer 30 og skrev ut svarene i konsollen.

Summen av de 30 første leddene er 67 455.

Ulike løsninger på denne oppgaven

Det finnes mange ulike løsninger på denne oppgaven – det viktigste er å passe på at ledd nr. 1 faktisk blir 1, ledd nr. 2 blir 2, ledd nr. 3 blir 6 og så videre. Derfor er det lurt å skrive ut alle leddene, og sjekke at de første leddene blir riktige sammelignet med oppgaveteksten. Her er ulike løsningsforslag til samme oppgave.

a = 1
sum = 0
for n in range(1, 31):
   a = a + (n - 1) ** 2  # regner ut nytt ledd
   sum = sum + a         # finner delsummen
   print(f"Ledd {n}: {a}. Delsum {n}: {sum}")

a = 1
sum = 1
for n in range(1, 30):
	a = a + n ** 2
	sum = sum + a
	print(f"Ledd {n + 1}: {a}. Delsum {n + 1}: {sum}")

a = 1
sum = 1
for n in range(2, 31):
   a = (n - 1) ** 2 + a  
   sum = sum + a         
   print(f"Ledd {n}: {a}. Delsum {n}: {sum}")


a = 1
sum = 1
for n in range(1, 31):
	print(f"Ledd {n}: {a}. Delsum {n}: {sum}")
	a = a + n ** 2
	sum = sum + a

Oppgave 2-5

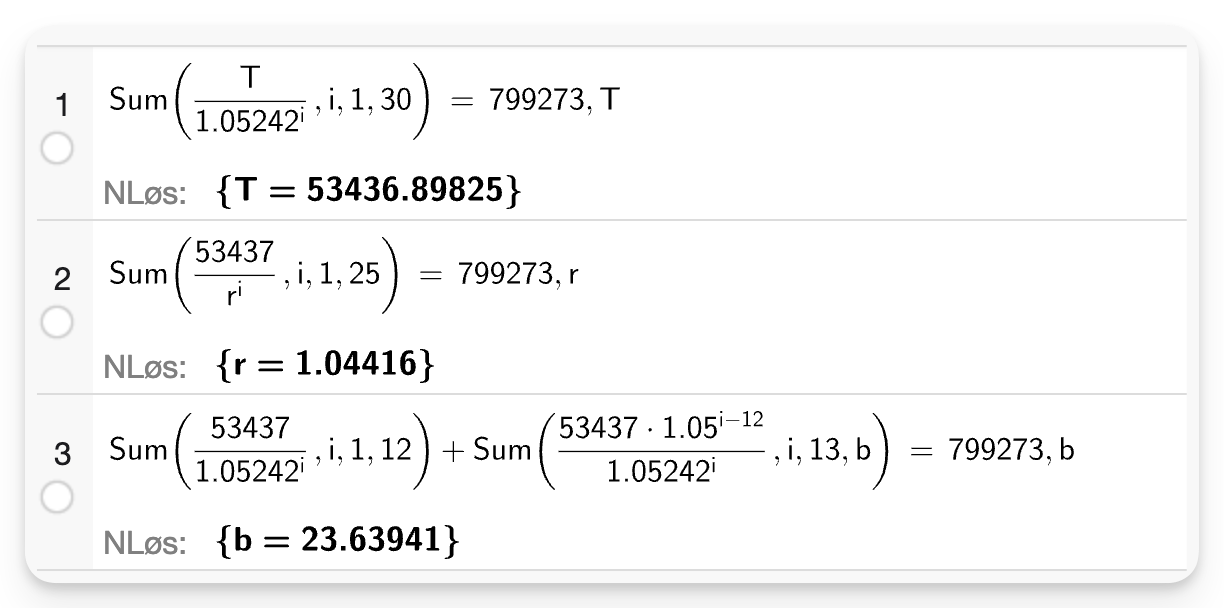
Løsning av oppgave 5 del 2 i CAS

a) Summen av nåverdiene til terminbeløpene skal være lik lånebeløpet ved annuitetslån. Terminbeløpet er ukjent, og dette ble funnet i linje 1 i GeoGebra. Lånebeløpet er 53 437 kr.
b) Summen av nåverdiene til terminbeløpene skal være lik lånebeløpet ved annuitetslån. Vekstfaktoren er ukjent, og denne ble funnet i linje 2 i GeoGebra. Rentesatsen må være 4,416 %.
c) Summen av nåverdiene til terminbeløpene skal være lik lånebeløpet ved annuitetslån. De 12 første årene bruker vi vanlig formel, de $b$ neste årene så vil terminbeløpet øke med 5 % per år. Antall ledd i rekka er ukjent, og dette ble bestemt i linje 3 i GeoGebra. Det tar 24 år før lånet er nedbetalt.

2-5 med Excel

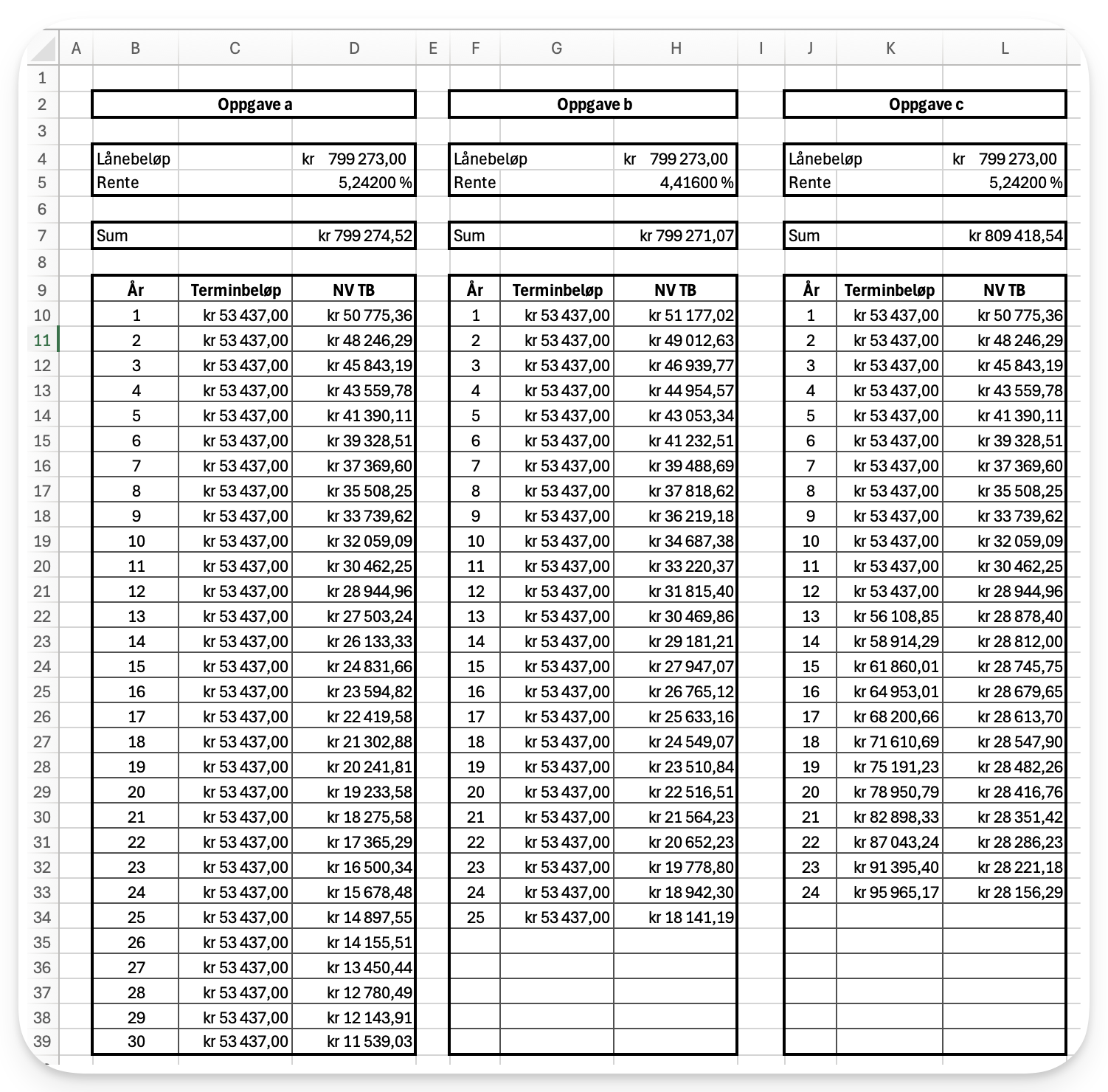
Vi kan løse hele denne oppgaven med Excel og målsøking. Se utklippet av regnearket

For å løse a) kan vi sette at alle terminbeløpene skal være lik det første terminbeløpet, og for å beregne nåverdien av terminbeløpet i celle D10 har jeg brukt formelen =(C10/(1+$D$5)^B10). Vi kan da bruke målsøking på terminbeløpet og sjekke hva det må være for at summen skal bli lik lånebeløpet. (Obs, jeg har rundet av svaret etter målsøking.)

For å løse b) kan vi gå ned til 25 terminer og bruke målsøking på renta hvis summen skal bli lik lånebløpet. (Obs, jeg har rundet av svaret etter målsøking.)

I oppgave c) så har jeg satt at terminbeløpet skal fra år 13 skal være 1,05 ganger det forrige terminbeløpet. Ved å markere cellene i kolonne L så kunne jeg lett finne ut at etter 24 år ble summen mer enn lånebeløpet. Jeg fjernet terminbeløpene etter år 24.

Løsning av oppgave 5 del 2 i Excel

Oppgave 2-6

Kostnadsfunksjon

I oppgaven får vi oppgitt en kostnadsfunksjon $K (x)$ , men jeg kan ikke se at vi har noen som helst bruk for den i løsningen.

2-6a

E (30) = 300 e^{- 0, 01 \cdot 30} = \underset{―}{\underset{―}{222, 2}}

Etterspørselen etter varen er 222,2 enheter når prisen er 30 kr per vare. Det betyr at vi kan forvente å selge 222 enheter dersom vi prisen varen til 30 kr.

2-6b

Vi lar etterspørselen $E (p)$ være lik $x$ (antall solgte varer), og løser med hensyn på $p$ , se linje 3 i GeoGebra.

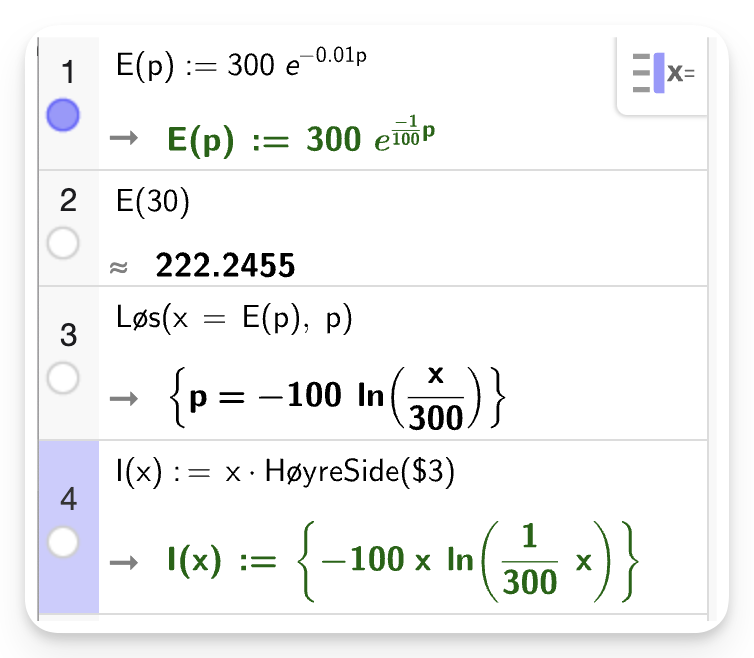
Løsning av oppgave 6 del 2 i CAS

Inntektene er gitt ved antall solgte varer $\times$ prisen per vare.

I (x) = x \cdot p = x \cdot (- 100 \ln (\frac{x}{300})) = \underset{―}{\underset{―}{- 100 x \ln (\frac{x}{300})}}