Løsningsforslag S2 eksamen H2025

Oppgave 1-1

Jeg ser at integranden er produktet av to funksjoner, og jeg velger derfor å bruke delvis integrasjon med DI-metoden.

	D	I
$+$	$x$	$e^{x}$
$-$	$1$	$e^{x}$
$+$	0

\int e^{x} \cdot x d x = x \cdot e^{x} - 1 \cdot e^{x} + C = \underset{―}{\underset{―}{e^{x} (x - 1) + C}}

Oppgave 1-2

1-2a

Vi kjenner $a_{1} = - 3$ og $a_{n} = 69$ , men vi kjenner ikke $n$ . Vi bruker derfor formelen for ledd i aritmetisk følge

\begin{aligned} a_{n} & = a_{1} + (n - 1) \cdot d \\ 69 & = - 3 + (n - 1) \cdot 3 \\ \frac{69}{3} & = \frac{- 3 + (n - 1) \cdot 3}{3} \\ 23 & = - 1 + (n - 1) \\ 23 + 1 + 1 & = n \\ n & = 25 \end{aligned}

Summen av den aritmetisk rekka er dermed

s_{n} = \frac{a_{1} + a_{n}}{2} \cdot n = \frac{- 3 + 69}{2} \cdot 25 = \frac{66}{2} \cdot 25 = 33 \cdot 25 = \underset{―}{\underset{―}{825}}

1-2b

Konvergensområdet er de verdiene av $x$ som tilfredsstiller $- 1 < k (x) < 1$ , der $k (x) = \frac{1}{2} - x$ .

\begin{aligned} - 1 & < k (x) < 1 \\ - 1 & < \frac{1}{2} - x < 1 \\ 1 & > - \frac{1}{2} + x > - 1 \\ 1 + \frac{1}{2} & > - \frac{1}{2} + x + \frac{1}{2} > - 1 + \frac{1}{2} \\ \frac{3}{2} & > x > - \frac{1}{2} \end{aligned}

Konvergensområdet for rekka er $\underset{―}{\underset{―}{x \in ⟨ - \frac{1}{2}, \frac{3}{2} ⟩}}$ .

1-2c

Ballen vil bevege seg på følgende måte:

$2$ m ned
$2 \cdot 0, 75 = 1, 5$ m opp
$2 \cdot 0, 75 = 1, 5$ m ned
$1, 5 \cdot 0, 75 = 1,125$ m opp
$1, 5 \cdot 0, 75 = 1,125$ m ned
Og så videre ...

Ballens totale distanse kan altså modelleres ved hjelp av to geometriske rekker, $a$ for distansen nedover, og $b$ for distansen oppover. Vi har $k = 0, 75$ , samt startverdiene $a_{1} = 2$ og $b_{1} = 1, 5$

\begin{aligned} s_{a} & = \frac{a_{1}}{1 - k} = \frac{2}{1 - \frac{3}{4}} = \frac{2}{\frac{1}{4}} = \frac{2 \cdot 4}{\frac{1}{4} \cdot 4} = \frac{8}{1} = 8 \\ s_{b} & = \frac{b_{1}}{1 - k} = \frac{1, 5}{1 - \frac{3}{4}} = \frac{1, 5}{\frac{1}{4}} = \frac{1, 5 \cdot 4}{\frac{1}{4} \cdot 4} = \frac{6}{1} = 6 \end{aligned}

Ballen vil totalt bevege seg 14 meter.

Oppgave 1-3

1-3a

Områder som ligger over $x$ -aksen vil ha identisk areal og integral. Områder som ligger under $x$ -aksen vil ha motsatt fortegn på integralet og arealet.

Vi deler derfor opp integrasjonen vår i to deler, en for området over $x$ -aksen (fra $x = - 2$ til $x = 0$ ), og en annen del for området under $x$ -aksen (fra $x = 0$ til $x = 1$ ).

Området fra $x = - 2$ til $x = 0$ ligger over $x$ -aksen, arealet og integralet er identiske. Området fra $x = 0$ til $x = 1$ ligger under $x$ -aksen, så arealet og integralet vil ha motsatt fortegn. For å beregne det samlede arealet må vi derfor endre fortegnet til integralet fra $x = 0$ til $x = 1$ , altså

\int_{- 2}^{0} f (x) d x - \int_{0}^{1} f (x) d x

Uttrykk 4 gir arealet markert på figuren.

1-3b

Jeg finner først det ubestemte integralet

F (x) = \int (x^{3} + x^{2} - 2 x) d x = \frac{1}{4} x^{4} + \frac{1}{3} x^{3} - \frac{2}{2} x^{2} + C

Arealet er gitt ved

\begin{aligned} A & = \int_{- 2}^{0} f (x) d x - \int_{0}^{1} f (x) d x \\ = {[F (x)]}_{- 2}^{0} - {[F (x)]}_{0}^{1} \\ = {[\frac{1}{4} x^{4} + \frac{1}{3} x^{3} - x^{2}]}_{- 2}^{0} - {[\frac{1}{4} x^{4} + \frac{1}{3} x^{3} - x^{2}]}_{0}^{1} \\ = ((0) - (\frac{1}{4} (- 2)^{4} + \frac{1}{3} (- 2)^{3} - (- 2)^{2})) - ((\frac{1}{4} 1^{4} + \frac{1}{3} 1^{3} - 1^{2}) - (0)) \\ = - (\frac{1}{4} \cdot 16 + \frac{1}{3} \cdot (- 8) - 4) - (\frac{1}{4} + \frac{1}{3} - 1) \\ = - (4 - \frac{8}{3} - 4) - (\frac{3}{12} + \frac{4}{12} - \frac{12}{12}) \\ = \frac{8}{3} - (- \frac{5}{12}) \\ = \frac{32}{12} + \frac{5}{12} = \frac{37}{12} \end{aligned}

Arealet er $\underset{―}{\underset{―}{\frac{37}{12}}}$ .

1-3c

Likningen til Kristian er sann når vi velger $a$ slik at vi får nøyaktig like store områder på oversiden og undersiden av $x$ -aksen.

Fra figuren kan vi se at Kristians beregning ser riktig ut, området som er avgrenset av $x$ -aksen og $f (x)$ fra $x = - 0, 6$ til $x = 1$ ser ut til å ha omtrent like mye areal over og under $x$ -aksen.

Hvis vi tar $\int_{- 2}^{1} f (x) d x$ så må svaret bli positivt siden det er mer areal på oversiden av $x$ -aksen.

Vi ser videre at $f (x)$ er negativ for $x < - 2$ , altså må det være mulig å velge en verdi for $a$ som er mindre enn $- 2$ slik at $\int_{a}^{1} f (x) d x = 0$ .

Hvis vi velger $a = - 2, 5$ så ser det ut til at vi har litt mer areal over $x$ -aksen enn under.
Hvis vi velger $a = - 3$ så ser det ut til at vi har litt mer areal under $x$ -aksen enn over.

Likningen til Kristian krever like mye areal på oversiden og undersiden av $x$ -aksen. Unni har rett i at det finnes to løsninger på likningen, der den andre løsningen ligger i intervallet $⟨ - 3, - 2, 5 ⟩$ .

Oppgave 1-4

1-4a

Jeg forutsetter at sannsynligheten er lik for alle fire sidene av terningen.

Farge	Gul	Grønn	Blå	Rød
$x$	$- 2$	$- 1$	$0$	$1$
$P (X = x)$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$	$\frac{1}{4}$
$x \cdot P (X = x)$	$- \frac{2}{4}$	$- \frac{1}{4}$	$0$	$\frac{1}{4}$
$(x - E (x))^{2}$	${(- \frac{3}{2})}^{2}$	${(- \frac{1}{2})}^{2}$	${(\frac{1}{2})}^{2}$	${(\frac{3}{2})}^{2}$
$(x - E (X))^{2} \cdot P (X = x)$	$\frac{9}{16}$	$\frac{1}{16}$	$\frac{1}{16}$	$\frac{9}{16}$

1-4b

E (X) = \sum x \cdot P (X = x) = - \frac{2}{4} + (- \frac{1}{4}) + 0 + \frac{1}{4} = - \frac{2}{4} = - \frac{1}{2}

$\underset{―}{\underset{―}{E (X) = - \frac{1}{2}}}$ . Det betyr at en spiller i gjennomsnitt vil tape 0,5 poeng per gang hen spiller i det lange løp.

1-4c

Var (X) = \sum (x - E (X))^{2} \cdot P (X = x)

Jeg har regnet ut hvert kvadratavvik i tabellen over.

Var (X) = \frac{9}{16} + \frac{1}{16} + \frac{1}{16} + \frac{9}{16} = \frac{20}{16} = \frac{5}{4}

Variansen $\underset{―}{\underset{―}{Var (X) = \frac{5}{4}}}$ .

Oppgave 1-5

1-5a

Når standardavviket er 5 cm så skal ca. 68 % av sannsynligheten ligge innenfor intervallet $⟨ 165, 175 ⟩$ og normalfordelingsfunksjonen skal ha toppunktet sitt ved $170$ cm. Vendepunktene til normalfordelingsfunksjonen skal også ligge ved $x = 165$ og $x = 175$ .

Figurene A og B viser fordelinger med standardavvik som er svært mye lavere enn 5 cm. Figur D viser et standardavvik som er mye høyere enn 5 cm.

Figur C passer til beskrivelsen.

1-5b

Vi lar $X$ være høyden til en tilfeldig valgt elev, og $\bar{X}$ være gjennomsnittshøyden til 25 tilfeldig valgte elever. Fra sentralgrensesetningen har vi at

\begin{aligned} E (\bar{X}) & = E (X) = 170 \\ SD (\bar{X}) & = \frac{SD (X)}{\sqrt{n}} = \frac{5}{\sqrt{25}} = \frac{5}{5} = 1 \end{aligned}

Vi ser at figur B har vendepunktene sine ved $x = 169$ og $x = 171$ .

Figur B passer til beskrivelsen.

Oppgave 2-1

2-1a

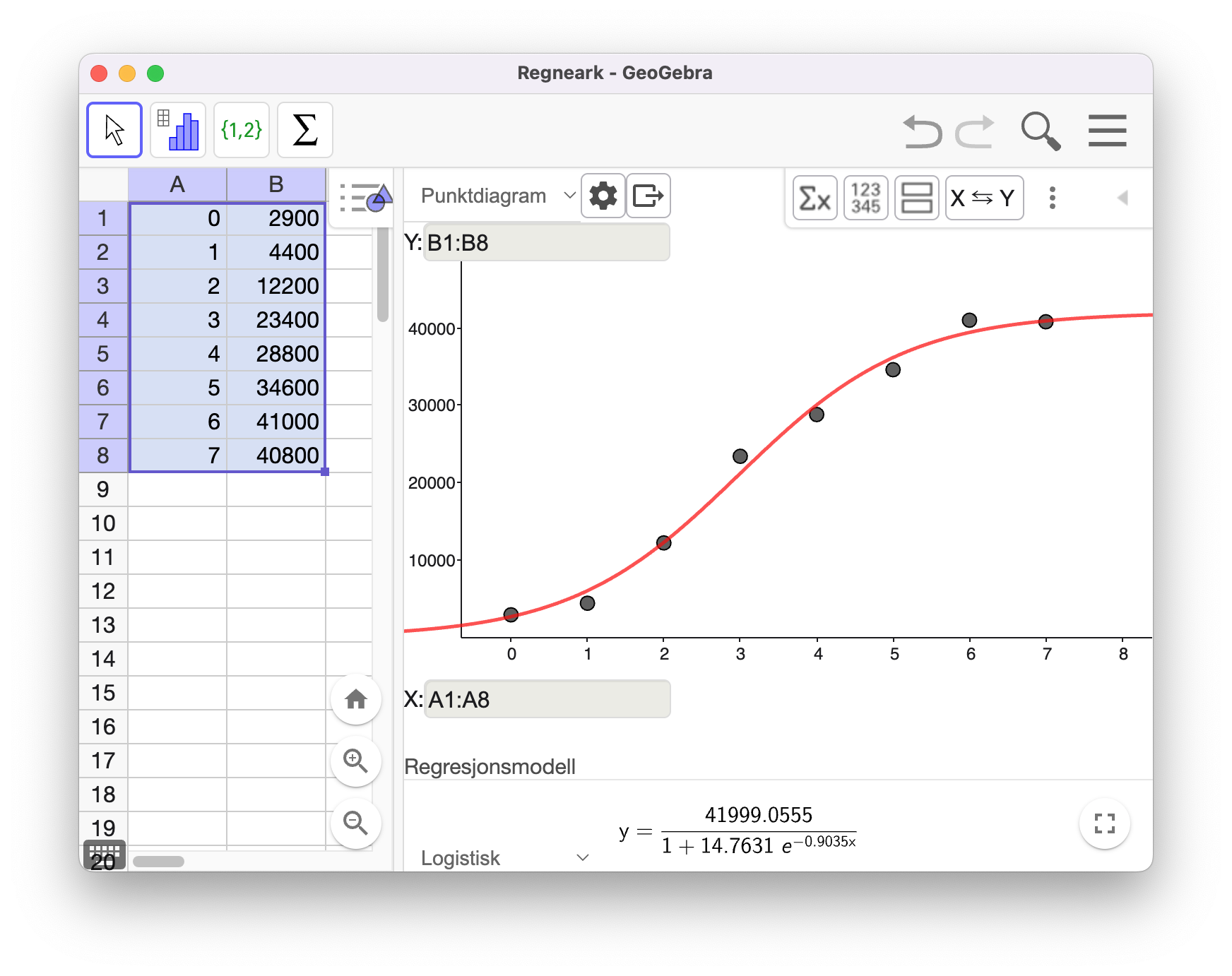
Regresjon i GeoGebra til oppgave 1 del 2

Jeg brukte regresjon i GeoGebra for å finne en logistisk modell som passer til uttrykket i oppgaveteksten. Den modellen som passer best er

\underset{―}{\underset{―}{I (t) = \frac{42 000}{1 + 14, 76 e^{- 0,903 5 t}}}}

Salget starter i uke 17, så modellen er ikke gyldig før dette. I uke 24 så ser vi at salget minker noe fra uke 23, og det er naturlig med tanke på at uke 24 er starten av sommerferien. Sannsynligvis selger man ikke like mye planter på sommeren som man gjør i vekstperioden på våren.

Jeg vurderer modellens gyldighetsområde til å kun være fra uke 17 til og med uke 24, altså $t \in [0, 7]$ .

2-1b

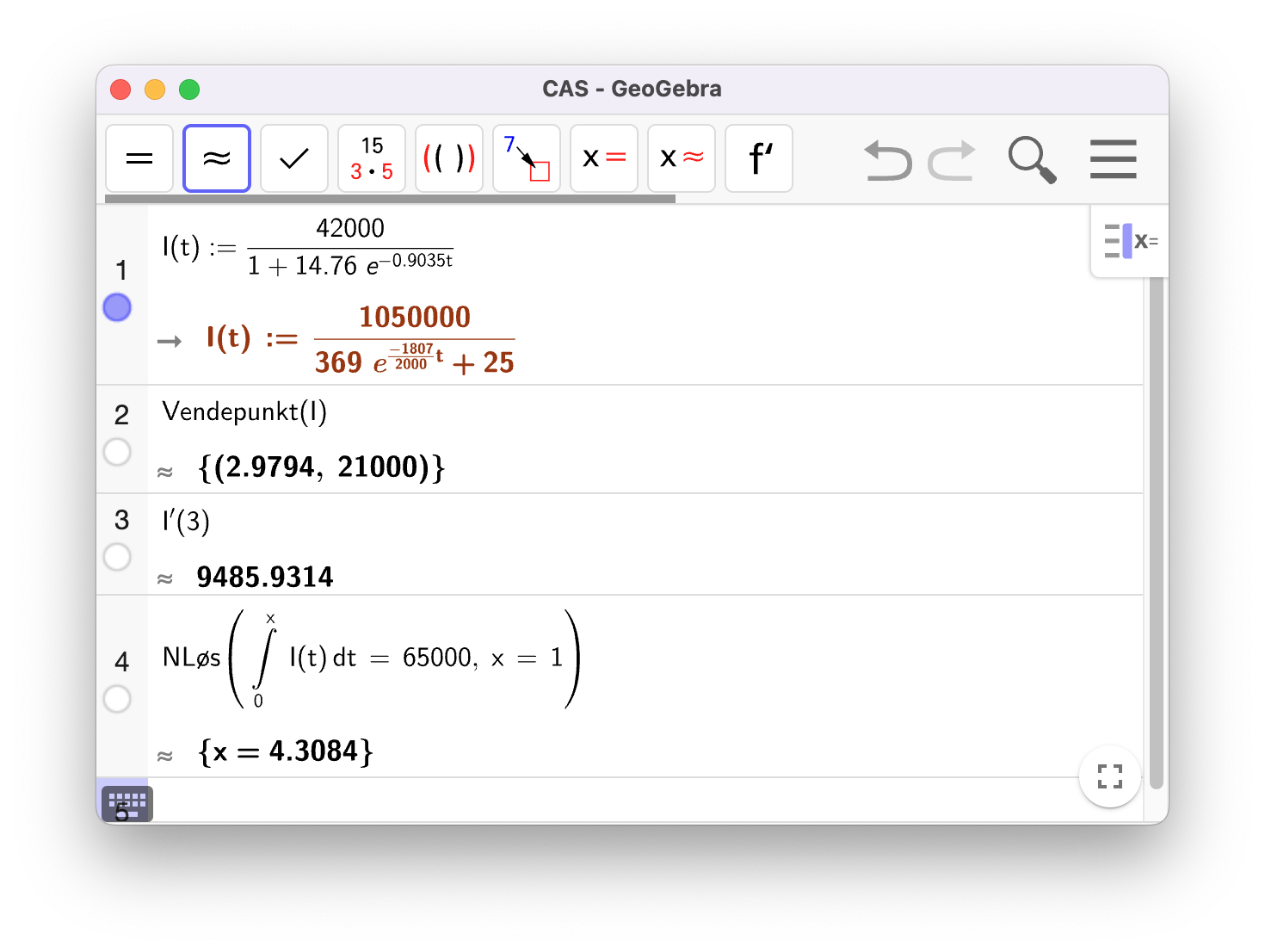
CAS løsning av oppgave 1 del 2

Inntekten øker mest ved vendepunktet $t = 3$ (etter 20 uker), se linje 2 i utklippet. Den deriverte til $I (t)$ gir oss vekstfarten etter 20 uker i linje 3.

Inntektene vokser raskest i uke 20. De vokser da med omtrent 9486 kr per uke.

2-1c

Se linje 4 i GeoGebra-utklippet. $x = 4, 3$ tilsvarer underveis i uke 21.

De samlede salgsinntektene for planten passerte 65 000 kr i uke 21.

Oppgave 2-2

Løsning i CAS av oppgave 2 del 2

2-2a

Se linje 2 i utklippet.

Grensekostnaden $K^{'} (150) = 7, 41$ . Kostnaden ved å øke produksjonen fra 150 enheter til 151 er omtrent 7,4 kroner.

2-2b

Enhetskostnadene er $E (x) = \frac{K (x)}{x}$ . Vi har lavest enhetskostnad når $E (x) = K^{'} (x)$ . Jeg satt opp likningen i linje 4 i utklippet og regnet ut enhetskostnaden i linje 5.

Vi har lavest enhetskostnader ved produksjon av 200 enheter. Da er enhetskostnaden 9,51 kroner.

2-2c

Jeg løser ulikheten $I > K$ i linje 7. Siden definisjonsmengden til $K$ er $D_{K} \in ⟨ 0, 500]$ så vil $I > K$ når $x \in [10, 500]$ .

Bedriften må produsere og selge fra og med 10 enheter til og 500 enheter for å gå med overskudd.

Oppgave 2-3

2-3a

Vi lar $p$ være sannsynligheten for at en tilfeldig valgt komponent er defekt. Bedriften som klager påstår at $p > 0, 01$ . Hypotesene våre er

\begin{array}{r} H_{0} : p \leq 0, 01 \\ H_{A} : p > 0, 01 \end{array}

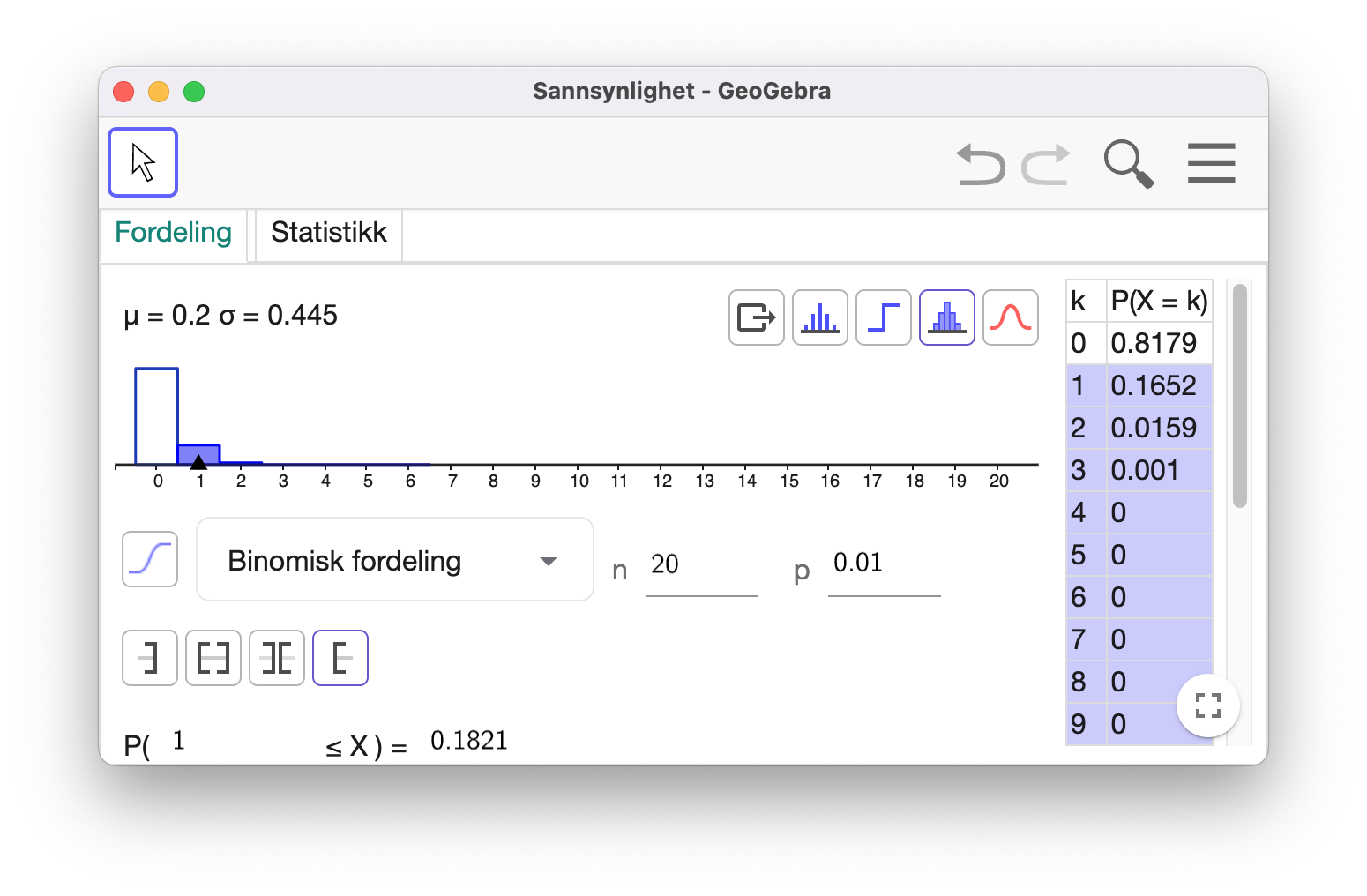
Binomisk hypotesetest til oppgave 3a del 2

Vi lar $X$ være antallet defekte komponenter når vi produserer 20 komponenter gitt at nullhypotesen vår er sann. Fra sannsynlighetsvinduet i GeoGebra har vi at

P (X \geq 1) = 0,182 1

Sannsynligheten for å finne 1 eller flere defekte komponenter gitt at nullhypotesen er sann er omtrent $18, 21 %$ .

$p$ -verdien er $0,182 1$ . Det er ikke grunnlag for forkaste nullhypotesen om at andelen er 1 % eller lavere. Klagen fra bedriften er ikke velbegrunnet.

2-3b

Usikker løsning

Jeg klarer ikke forstå hva oppgaven spør etter. Jeg er ikke sikker på at dette er riktig løsning.

Nullhypotesen er fremdeles $H_{0} : p \leq 0, 01$ .

Kontrolløren har kontrollert $n$ komponenter. Det skal maksimalt være 5 % sannsynlighet for at han «var så heldig» at han bare fant 0 eller 1 defekt komponent. Vi skal altså finne den minste verdi for $n$ som gjør at $P (X \leq 1) < 0, 05$ , gitt at $p = 0, 01$ .

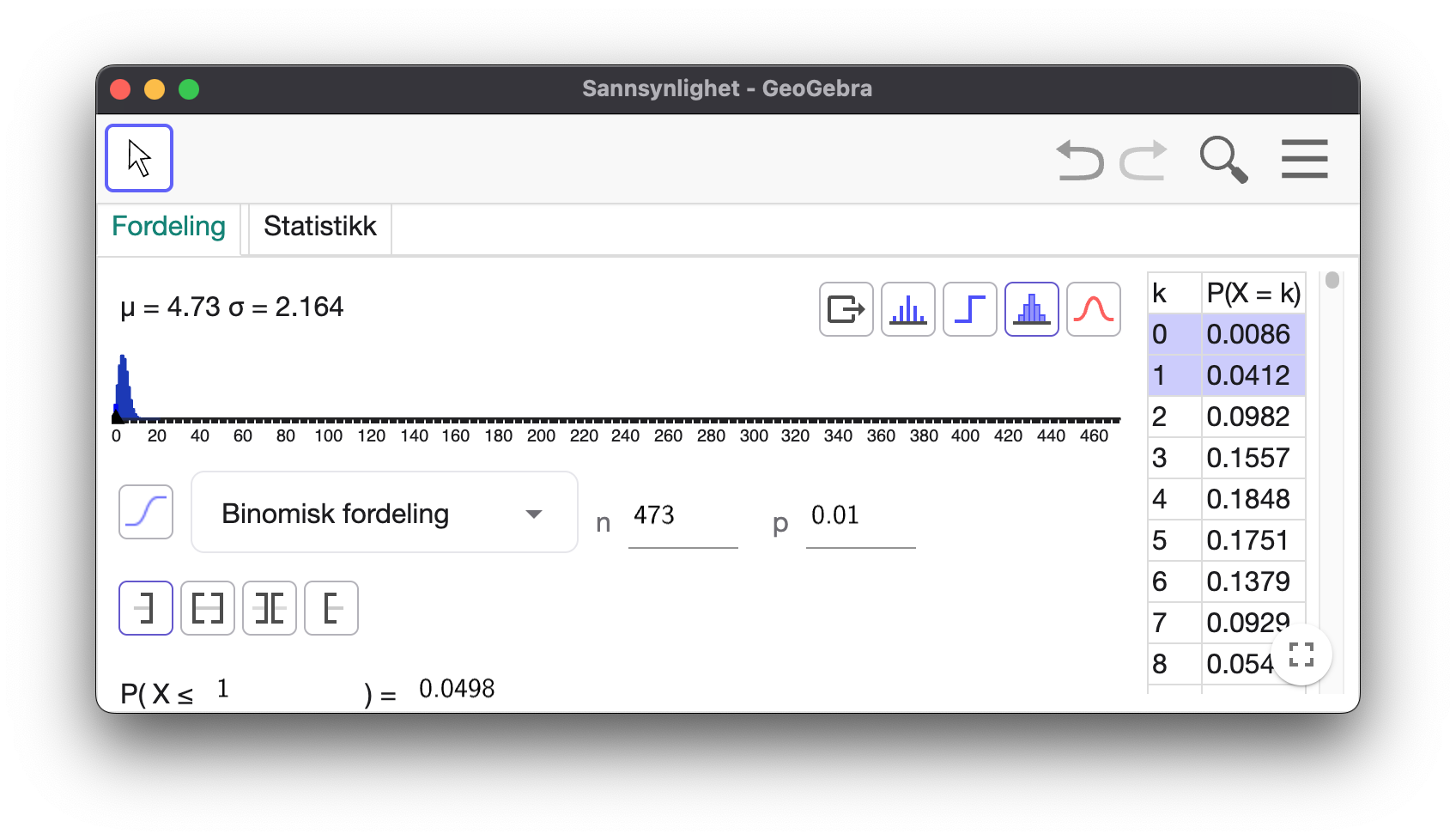
Binomisk hypotesetest til oppgave 3b del 2

Ved å endre på $n$ finner jeg fort ut at

Ved $n = 472$ så er $P (X \leq 1) = 0,050 2$
Ved $n = 473$ så er $P (X \leq 1) = 0,049 8$

Hvis kontrolløren kontrollerte 473 komponenter, så er sannsynligheten for å kun finne 0 eller 1 defekte komponenter 4,98 %.

Kontrolløren må minst ha kontrollert 473 komponenter.

Oppgave 2-4

Løsning av oppgave 4 del 2 i CAS

2-4a

Et annuitetslån passer godt til oppgaven siden den spør etter en geometrisk rekke som viser hvor mye Mathias må betale.

I et annuitetslån må summen av nåverdiene til terminbeløpene tilsvare lånebeløpet, altså

\sum_{i = 1}^{8} \frac{T}{1, 04^{i}} = 357 000

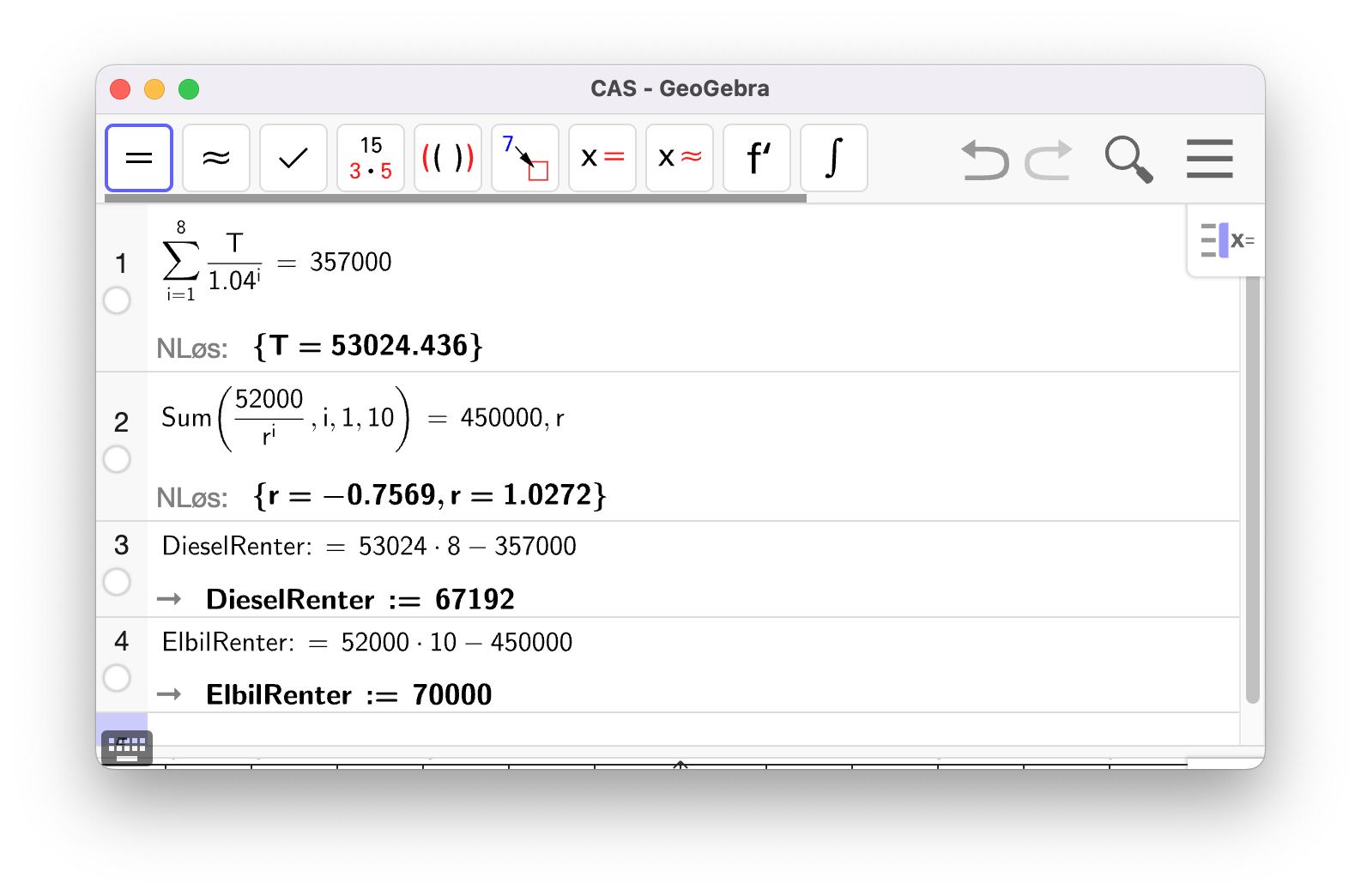
Jeg løser denne i CAS (se linje 1).

Terminbeløpene er 53 024 kr.

2-4b

Siden det er fast terminbeløp på 52 000 kr, så vil også dette lånet være et annuitetslån.

Jeg setter opp likningen i CAS og løser (se linje 2). Vekstfaktoren er $1,027 2$ (vi ser bort fra den negative løsningen da vekstfaktorer alltid er positive), dette gir $2, 72 %$ rente.

Rentesatsen er 2,72 %.

2-4c

Rentekostnadene er summen av terminbeløpene minus prisen på bilene. Disse har jeg beregnet i linje 3 og 4 i utklippet.

Å kjøpe elbilen vil gi høyest rentekostnader totalt, men det er først og fremst på grunn av at elbilen er dyrere og nedbetalingstiden er lengre. Rentesatsen er lavest for elbilen.

Oppgave 2-5

Den rekursive sammenhengen kan skrive matematisk som $B_{n + 1} = B_{n} + 3 + n$ , der $n \geq 1$ og $B_{1} = 1$ .

Vi kan også beskrive sammenhengen som at sparingen starter på 1 krone og at sparingen øker med 4 kroner til dag 2. Deretter øker sparingen med 1 krone mer per dag. Jeg velger å bruke dette mønsteret til programmeringen.

sparing = 1             # daglig sparebeløp i starten
økning = 4              # den første økningen
sum_spart = sparing     # sum på sparekontoen
dag = 1                 # dag nummer

while sum_spart < 100_000:
    dag = dag + 1                       # ny dag
    sparing = sparing + økning          # nytt sparebeløp 
    sum_spart = sum_spart + sparing     # setter inn beløpet på konto
    økning = økning + 1                 # beregner økningen til neste dag

print(f"Etter {dag} dager har Wiggo spart over 100 000 kr. Han har da spart {sum_spart} kr.")

Output: Etter 82 dager har Wiggo spart over 100 000 kr. Han har da spart 101926 kr.

Oppgave 2-6

2-6a

I denne oppgaven er jeg veldig usikker på hva som kreves for å forklare at uttrykket i oppgaveteksten er det samme som forventningsverdien. Jeg tror ikke det er meningen at elever skal gjøre det samme som jeg har gjort her – men jeg klarer ikke helt å se en enklere måte å argumentere for at forventningsverdien er eksakt lik summen av «antall kast nødvendig».

Valgtre til oppgave 6 del 2

Vi lar $X$ være antall kast som trengs før vi har fått 2 like terningkast på rad. Sannsynligheten for å at et terningkast har samme antall øyne som det forrige er $1 / 6$ , og sannsynligheten for at antall øyne er ulikt er $5 / 6$ . Vi kan bruke multiplikasjonsprinsippet og sette opp følgende sannsynlighetsfordeling for $X$ :

$x_{i}$	$P (x_{i})$
$1$	$0$
$2$	$\frac{1}{6}$
$3$	$\frac{5}{6} \cdot \frac{1}{6}$
$4$	${(\frac{5}{6})}^{2} \cdot \frac{1}{6}$
$5$	${(\frac{5}{6})}^{3} \cdot \frac{1}{6}$

Forventningsverdien til $X$ vil da være

\begin{aligned} E (X) & = lim_{n \to \infty} \sum_{i = 1}^{n} x_{i} \cdot P (x_{i}) \\ = 1 \cdot 0 + 2 \cdot \frac{1}{6} + 3 \cdot \frac{5}{6} \cdot \frac{1}{6} + 4 \cdot {(\frac{5}{6})}^{2} \cdot \frac{1}{6} + 5 \cdot {(\frac{5}{6})}^{3} \cdot \frac{1}{6} + \dots \\ = \frac{1}{6} (\underset{S}{\underset{⏟}{2 {(\frac{5}{6})}^{0} + 3 {(\frac{5}{6})}^{1} + 4 {(\frac{5}{6})}^{2} + 5 {(\frac{5}{6})}^{3} + \dots}}) \end{aligned}

Vi kaller alt inni parentesen for $S$ , og omskriver heltallene som står foran $\frac{5}{6}$ som en sum av enere:

\begin{array}{r} S = \underset{2}{\underset{⏟}{(1 + 1)}} \cdot {(\frac{5}{6})}^{0} + \underset{3}{\underset{⏟}{(1 + 1 + 1)}} \cdot {(\frac{5}{6})}^{1} \underset{4}{\underset{⏟}{(1 + 1 + 1 + 1)}} \cdot {(\frac{5}{6})}^{2} + \dots \end{array}

Vi deler nå opp denne summen i en rekke delsummer slik at $S = lim_{n \to \infty} S_{1} + S_{2} + \dots + S_{n}$ hvor

\begin{aligned} S_{1} & = 1 \cdot {(\frac{5}{6})}^{0} + 1 \cdot {(\frac{5}{6})}^{1} + 1 \cdot {(\frac{5}{6})}^{2} + \dots = \frac{1}{1 - \frac{5}{6}} = \frac{1}{\frac{1}{6}} = 6 \\ S_{2} & = 1 \cdot {(\frac{5}{6})}^{0} + 1 \cdot {(\frac{5}{6})}^{1} + 1 \cdot {(\frac{5}{6})}^{2} + \dots = \frac{1}{1 - \frac{5}{6}} = \frac{1}{\frac{1}{6}} = 6 \\ S_{3} & = 1 \cdot {(\frac{5}{6})}^{1} + 1 \cdot {(\frac{5}{6})}^{2} + 1 \cdot {(\frac{5}{6})}^{3} + \dots \frac{\frac{5}{6}}{1 - \frac{5}{6}} = \frac{\frac{5}{6}}{\frac{1}{6}} = 5 \\ S_{4} & = 1 \cdot {(\frac{5}{6})}^{2} + 1 \cdot {(\frac{5}{6})}^{3} + 1 \cdot {(\frac{5}{6})}^{4} + \dots = \frac{{(\frac{5}{6})}^{2}}{1 - \frac{5}{6}} = \frac{{(\frac{5}{6})}^{2}}{\frac{1}{6}} = 6 \cdot {(\frac{5}{6})}^{2} \\ S_{5} & = 1 \cdot {(\frac{5}{6})}^{3} + 1 \cdot {(\frac{5}{6})}^{4} + 1 \cdot {(\frac{5}{6})}^{5} + \dots = \frac{{(\frac{5}{6})}^{3}}{1 - \frac{5}{6}} = \frac{{(\frac{5}{6})}^{3}}{\frac{1}{6}} = 6 \cdot {(\frac{5}{6})}^{3} \end{aligned}

Forventningsverdien er altså

\begin{aligned} E (X) & = \frac{1}{6} S \\ = \frac{1}{6} (S_{1} + S_{2} + S_{3} + S_{4} + S_{5} + \dots) \\ = \frac{1}{6} (6 + 6 + 5 + 6 \cdot {(\frac{5}{6})}^{2} + 6 \cdot {(\frac{5}{6})}^{3} + \dots) \\ = 1 + 1 + \frac{5}{6} + {(\frac{5}{6})}^{2} + {(\frac{5}{6})}^{3} + \dots & ◼ \end{aligned}

Hvis vi ser bort fra det aller første leddet ( $1$ ), så er dette en uendelig geometrisk rekke med $a_{1} = 1$ og $k = \frac{5}{6}$

s = 1 + \frac{5}{6} + {(\frac{5}{6})}^{2} + \dots

Vi kan finne summen av rekka $s$ med GeoGebra, eller med formelen for sum av uendelig geometrisk rekke:

s = \frac{1}{1 - \frac{5}{6}} = \frac{1}{\frac{1}{6}} = \frac{1 \cdot 6}{\frac{1}{6} \cdot 6} = 6

Til sammen blir altså $E (X) = 1 + s = 1 + 6 = 7$ .

Verdien av rekka er 7.

2-6b

Vi skal simulere forventningsverdien til summen av antall øyne på alle terningene som kastes i jakten på å få to like kast på rad.

from random import randint
N = 100_000                        
sum_øyne = 0                        # totalt antall øyne på terningene

for i in range(N):
    t1 = randint(1,6)               # terningkast 1
    t2 = randint(1,6)               # terningkast 2

    sum_øyne = sum_øyne + t1 + t2   # legger til resultatene til summen
    while t1 != t2:
        t1 = t2                     # flytter t2's verdi til t1
        t2 = randint(1,6)           # ruller t2 på nytt
        sum_øyne = sum_øyne + t2    # legger til nytt resultat til summen

EX = sum_øyne/N                     # forventningsverdi = snitt i det lange løp
print(f"Jeg estimerer forventningsverdien til å være {EX:.3f} etter {N} simuleringer.")

Output: Jeg estimerer forventningsverdien til å være 24.502 etter 100000 simuleringer.

Etter å ha kjørt programmet flere ganger ser det ut til estimatet mitt er stabilt på rundt $24, 5$ . Det stemmer også godt med at forventningsverdien for en terning er $3, 5$ og vi trenger i snitt $7$ kast før vi har fått to like på rad.

Jeg estimerer forventningsverdien til summen av antall øyne før Ane får to like terninger på rad til å være 24,5.