Løsningsforslag S2 eksamen V2016

Oppgave 2-4

2-4a

For å finne ut hvor stort engangsbeløp foreldrene må betale så kan jeg sette opp en likning. Jeg lar $x$ kr være engangsbeløpet, vekstfaktoren til 2,5 % rente er 1,025 og vi skal la pengene stå på konto i 18 år.

\begin{aligned} x \cdot {1,025}^{18} & = 100 000 \\ x & = \frac{100 000}{{1,025}^{18}} = 64 116, 16 \end{aligned}

Foreldrene må sette inn 64 116,16 kr for når Ole Magnus blir født, for at beløpet skal være 100 000 kr når han blir 18 år med 2,5 % årlig rente.

2-4b

Løsning med CAS

Jeg tenker på dette som en rekke med 18 ledd (18 innbetalinger). Den første innbetalingen skjer når Ole Magnus er 0 år. Hvis vi lar $x$ kr være det årlige beløpet så vil den første innbetalingen ha forrentet seg til

x \cdot {1,025}^{18}

etter 18 år. Den siste innbetalingen (som ble gjort da Ole Magnus fylte 17 år) vil ha forrentet seg til

x \cdot {1,025}^{1}

Vi kan altså se på dette som en endelig geometrisk rekke med første ledd $a_{1} = x \cdot {1,025}^{1}$ og $k = 1,025$ .

Jeg bruker Sum-funksjonen i CAS og skriver inn Sum(x*1.025^(i),i,1,18)=100000. CAS gir svaret $x = 4358, 06$ .

Foreldrene må sette inn 4358,06 kr hvert år dersom Ole Magnus skal ha 100 000 kr på kontoen når han fyller 18 år med 2,5 % årlig rente.

Løsning med sumformel

Oppgaveteksten ber oss løse oppgaven med CAS. Jeg tolker dette som at jeg skal bruke Sum-funksjonen i CAS, men det er også mulig å bruke sumformel for geometrisk rekke og sette opp likningen

x \cdot 1.025 \cdot \frac{{1.025}^{18} - 1}{1.025 - 1} = 100000

Løsning med Excel

For å løse denne oppgaven i Excel satte jeg opp et regneark med 18 innbetalinger. Jeg tok også med en rad for det året Ole Magnus fylte 18 år, men dette året var uten innbetaling.

For hvert år regnet jeg ut ny saldo med renter ved å multiplisere forrige års saldo med vekstfaktoren. I tillegg lag jeg til årets innskudd. Se formlene jeg har brukt i G6 og nedover.

For å finne riktig årlig beløp brukte jeg Målsøking-funksjonen, og ba Excel finne ut hva celle C5 måtte endres til slik at celle G23 ble 100 000 kr.

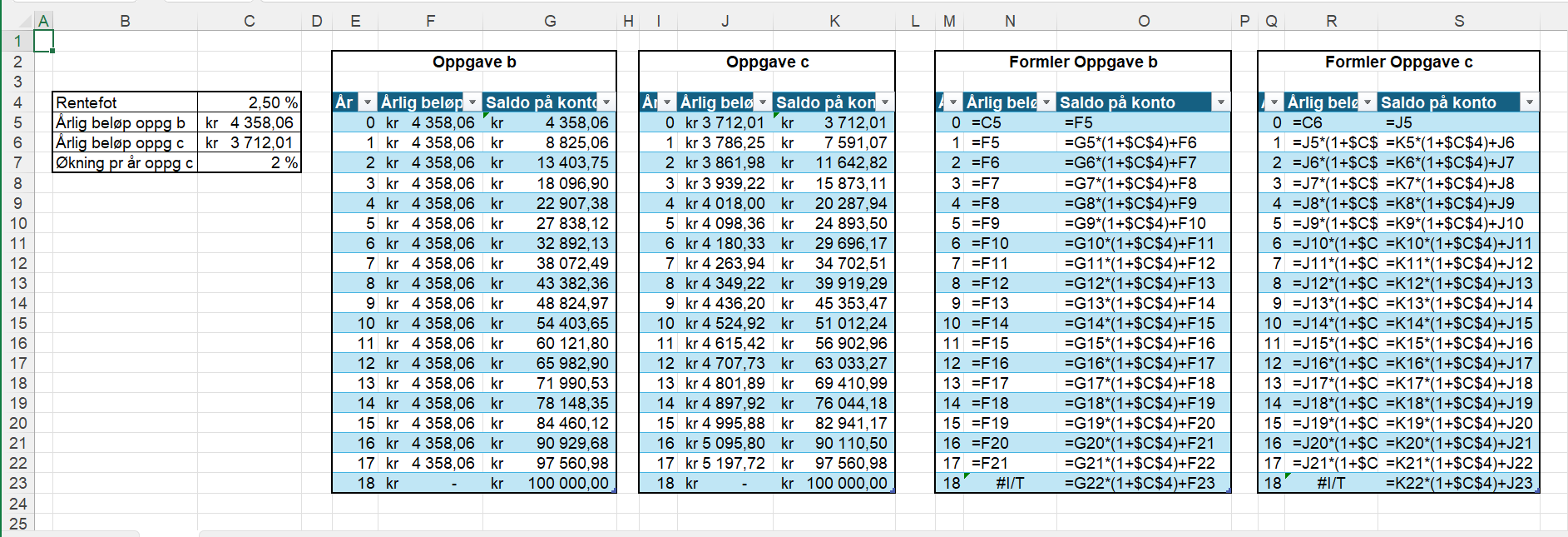
2-4c

Løsning i CAS

Jeg lar $x$ kr være det første beløpet som settes inn. Jeg ser at det vil forrentes til $x \cdot {1,025}^{18}$ . Det andre beløpet vil kun få 17 år med renter, men det vil samtidig være 2 % større enn det første beløpet. Jeg kan skrive det andre og tredje beløpet som

\begin{array}{r} x \cdot {1,025}^{17} \cdot 1, 02^{1} \\ x \cdot {1,025}^{16} \cdot 1, 02^{2} \end{array}

Når jeg legger sammen leddene får jeg en rekke. Jeg finner ut hva $x$ må være ved å sette rekka lik 100 000 i CAS med kommandoen Sum(x*1.02^(i-1)*1.025^(19-i),i,1,18)=100000 og trykker på x≈. Det er det samme som å løse likningen

\sum_{i = 1}^{18} x \cdot {1.02}^{i - 1} \cdot {1.025}^{19 - i} = 100000

CAS gir meg svaret $x = 3712, 01$

Ved å sette inn 3712,01 kr når Ole Magnus blir født, vil han motta 100 000 kr når han blir 18 år gammel, dersom innskuddsbeløpet økes med 2 % per termin og renta er 2,5 %.

Løsning med Excel

Se utklippet over. Jeg endret på formelen for innskuddsbeløpet fra oppgave b, slik at innskuddsbeløpet alltid er 1,02 ganger større enn fjorårets innskudd. I J8 står det for eksempel =J7*(1+$C$7).

For å finne riktig årlig beløp brukte jeg Målsøking-funksjonen, og ba Excel finne ut hva celle C6 måtte endres til slik at celle K23 ble 100 000 kr.